Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 164
Substitua as duas forças atuando no mastro por um torçor. Escreva na forma vetorial o momento associado com o torçor e especifique as coordenadas do ponto no plano - pelo qual passa a linha de ação do torçor.
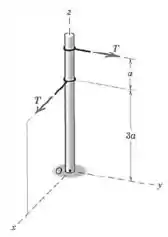
Passo 1
Vamos começar calculando a força resultante. Para isso precisamos escrever cada força em forma vetorial:
E então a força resultante é:
Já que vamos montar um torçor, vamos precisar do vetor unitário na direção de , e é uma boa calculá-lo de uma vez:
Passo 2
Agora vamos calcular o momento associado a essas forças. A tensão que atua mais acima produz rotação em torno do eixo , no sentido horário:
E a tensão que atua mais abaixo produz rotação em torno do eixo , no sentido anti-horário:
Então o momento total é:
Passo 3
Agora queremos substituir as duas forças atuando no mastro por um torçor. Podemos definir totalmente esse torçor se especificarmos as coordenadas do ponto de aplicação, e qual é o momento associado.
Sabemos que o torçor, para ser equivalente à força que vai substituir, precisa satisfazer a seguinte equação:
Onde é o vetor posição que liga a origem ao ponto de ação no plano -. Temos os seguintes vetores:
E é um vetor paralelo ao , e aqui podemos aproveitar o vetor unitário que calculamos no passo :
Passo 4
Agora vamos tentar resolver essa equação:
O primeiro passo é resolver o produto vetorial do lado direito:
E substituindo isso de volta na equação principal:
Agora vamos igualar cada componente:
E podemos usar esse sistema para encontrar e .
E vamos substituir a segunda equação na primeira:
Passo 5
Agora podemos usar qualquer uma daquelas equações para calcular o módulo do momento :
Substituindo :
E então o vetor é:
Resposta
As coordenadas são e . O momento é .