Represente por uma única força , em e por um momento a resulatnte do sistema de forças atuando em um conjunto de tubos.
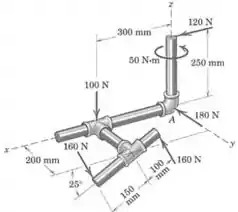
Passo 1
Vamos começar calculando a força resultante. As duas forças de se anulam perfeitamente, então não precisamos considerá-las na conta.
Então a força resultante é a seguinte:
Passo 2
Agora vamos calcular os momentos. Começando pelo par de forças de , que formam um binário separado por .
E esse momento é em torno do eixo , no sentido anti-horário:
E como as outras três forças são paralelas aos eixos, podemos calcular os seus momentos sem fazer nenhuma conta muito complicada.
A força de produz rotação em torno do eixo , no sentido anti-horário:
A força de também produz rotação em torno do eixo , e mais uma vez no sentido anti-horário:
Como a força de tem sua linha de ação passando pelo ponto , ela não produz momento.
Passo 3
Agora podemos somar todos esses momentos (além do momento de em torno do eixo ) para encontrar o momento total:
Resposta
A força resultante é e o momento resultante é .