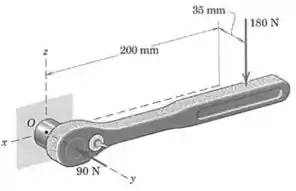
Ao apertar um parafuso cujo centro está no ponto , uma pessoa exerce, com a mão direita, uma força de no manete da chave de catraca. Além disso, com a mão esquerda exerce uma força de , como mostrado, para manter o soquete na cabeça do parafuso. Determine o sistema força-binário equivalente em . Determine, então, o ponto no plano - pelo qual passa a linha de ação da força resultante do torçor.

Agora queremos calcular o momento em relação ao ponto . Como a linha de ação da força de passa pelo ponto , o momento dela é nulo, e só precisamos nos preocupar com o momento da força de .

Essa força é paralela ao eixo , e sua linha de ação não cruza nenhum dos outros dois eixos, por isso ela vai gerar momento em relação a e .

Em torno do eixo o momento favorece a rotação no sentido horário, e por isso colocamos um sinal negativo:

E o mesmo acontece para a rotação em torno do eixo :

E então o momento total é:

Agora queremos calcular as coordenadas pela qual passa a linha de ação da força resultante do torçor.

Como estamos lidando com um torçor, a equação que vamos usar para descobrir essas coordenadas é a seguinte:

Onde é um vetor momento paralelo à força resultante :

E então vamos precisar encontrar o vetor unitário na direção de :

E o nosso vetor é:

Vamos voltar à nossa equação:

E agora substituimos também a expressão que encontramos para e :

E então podemos escrever algumas equações:

Podemos resolver a primeira para encontrar o valor de :

E vamos substituir a terceira equação na segunda para encontrar o valor de :