Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 154
O motor montado na cantoneira suporta seu peso de e seu eixo resiste ao empuxo de e ao torque de aplicados. Determine a resultante do sistema de forças mostrado em termos de uma força em e de um torque .
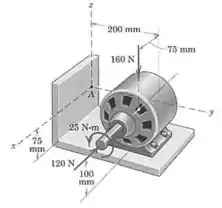
Passo 1
Vamos começar calculando a força resultante. Para isso precisamos escrever cada força em forma vetorial:
E então a força resultante é:
Passo 2
Se a resultante dessas forças for aplicada em , todo o momento que as forças geravam vai sumir. Para que o efeito sobre o motor continue o mesmo, precisamos calcular qual era o momento dessas forças em relação a .
A força de (força ) vai produzir rotação em torno dos eixos e :
E o sinal negativo aparece em porque esse momento favorece rotação no sentido horário.
E a força de (força ) vai produzir rotação em torno dos eixos e :
E mais uma vez o sinal negativo aparece no momento que favorece a rotação no sentido horário.
Passo 3
Agora podemos calcular o momento total dessas forças (lembrando de adicionar o momento de em torno de que está representado na figura):
Resposta
A força resultante é e o momento total é .