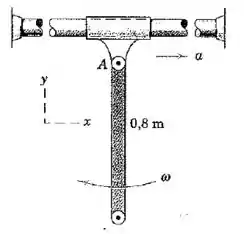
A extremidade da barra uniforme de é livremente articulada no cursor, que possui uma aceleração ao longo do eixo horizontal fixo. Se a barra tem uma velocidade angular no sentido horário quando passa pela posição vertical, determine as componentes da força sobre a barra em para esse instante.
Passo 1
Pelos dados do enunciado já podemos fazer várias afirmações sobre as forças resultantes que agem sobre a barra:
Primeiro, se a barra tem uma velocidade angular em torno do ponto , isso já garante que existe uma força centrípeta agindo sobre o centro de massa da barra, e que aponta na direção de :
Essa força é vertical para cima.
Segundo, como o sistema se move para a direita com aceleração , existe uma força apontando para a direita agindo no centro de maassa:
Essa força é horizontal para a direita.
Terceiro, existe uma força na direção tangencial ao movimento circular da barra, que produz a sua rotação em torno de :
Essa força é horizontal para a esquerda.
Então quando escrevemos a segunda lei de Newton em cada uma das direções, vamos encontrar o seguinte:
Passo 2
Agora vamos representar analisar a soma das forças que agem sobre a barra. Temos apenas as componentes e da força em , e o peso :
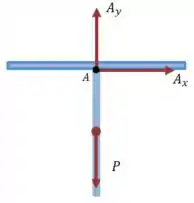
Vamos substituir isso nas equações que escrevemos ali em cima. Começando pela vertical:
E na horizontal:
Fica faltando encontrar a aceleração angular .
Passo 3
Podeos fazer isso usando uma equação de momentos em relação ao ponto .
O primeiro termo da direita é fácil de calcular, basta usar a expressão do momento de inércia em relação à extremidade da barra:
E o segundo termo é apenas o momento das forças resultante sobre o centro de massa em relação ao ponto :
Então:
Agora é só substituir na equação que escrevemos antes:
Resposta
As componentes das forças são (horizontal para a direita) e (vertical para cima).