Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 95
A casca semicilíndrica uniforme de massa e raio é liberada a partir do repouso na posição mostra, com sua borda inferior apoiada sobre a superfície horizontal. Determine o coeficiente de atrito estático mínimo que é necessário para evitar qualquer deslizamento inicial da casca.
Passo 1
Vamos começar fazendo um esquema para a visão “em perfil” da casca:
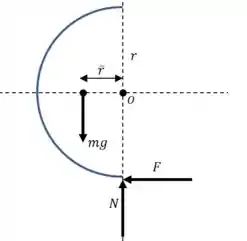
Vamos começar encontrando o momento de inércia em relação ao centro de massa; Usando o teorema dos eixos paraleos podemos escrever o seguinte:
E o momento de inércia em relação ao ponto é tabelado:
E a posição do centro de massa também é tabelada:
Passo 2
Beleza, com essa informação vamos escrever uma equação para o momento em relação ao centrode massa:
E as forças que produz momento em relação ao centro de massa são (força de atrito) e :
Ok, essa é nossa primeira equação. Precisamos de mais duas para ficar com um sistema de três variáveis (, e ) e três equações.
Passo 3
Para encontrar essas duas equações vamos usar a segunda lei de Newton:
A única força que age na direção horizontal é :
E qual é a componente da aceleração do centro de massa nessa direção?
E agora vamos para a direção vertical:
E a componente da aceleração do centro de massa nessa direção está associada à rotação em torno do centro de massa.
É importante lembrar que estamos considerando o instante inicial, na posição mostrada no desenho. Em outros instantes, essa aceleração teria outras direções, mas aqui ela é vertical para baixo.
Então:
Passo 4
Ótimo, já temos um sistema de três equações e três variáveis.
Lembrando que nosso objetivo é encontrar , que obedece a seguinte relação:
Então vamos começar a resolver:
Começamos substituindo a primeira e a segunda equações na terceira e dividindo tudo por :
Agora que temos , vamos fazer a razão que dá :
E substituindo que encontramos:
Divivindo tudo por e multiplicando tudo por :
Resposta
O coeficiente de atrito estático mínimo deve ser .