Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 86
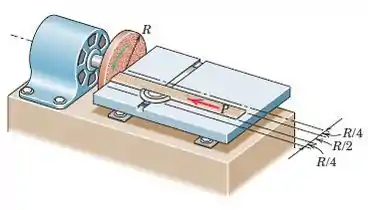
Uma extremidade da placa fina está sendo lixada pela lixadeira de disco sob a aplicação da força P. Se o coeficiente efetivo de atrito cinético for μ e se a pressão for essencialmente constante sobre a extremidade da placa, determine o momento M que deve ser aplicado por o motor para girar o disco a uma velocidade angular constante. A extremidade da placa é centralizada ao longo do raio do disco.
Passo 1
Primeiro, vamos desenhar a projeção yOz do diagrama de corpo livre do disco, com a pressão P, o atrito F e o par M atuando nele
Podemos escrever a força de atrito como
Passo 2
A seguir, desenharemos a projeção xOy do diagrama de corpo livre do disco
Uma vez que o coeficiente de atrito é constante e a pressão P atua no centro da placa, podemos assumir que a força de atrito total F também atua no centro da placa
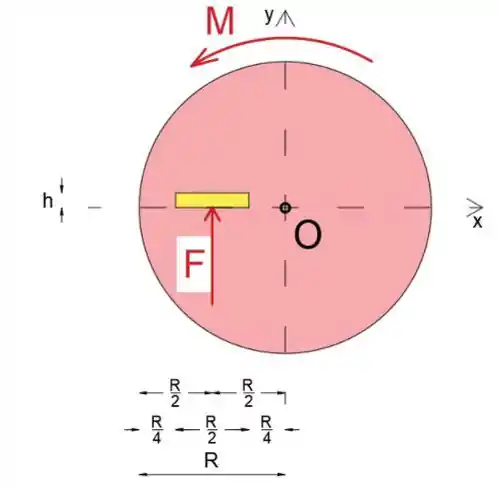
Passo 3
Ao igualar a soma dos momentos sobre o ponto 0 a zero, podemos escrever a expressão para o momento M
Substituiremos F por