Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 23
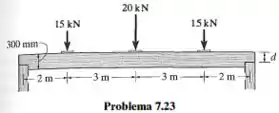
As extremidades da viga de madeira devem ser entalhadas como mostra a figura. Se a viga tiver de suportar o carregamento mostrado, determine a menor profundidade d da viga no entalhe se a tensão de cisalhamento admissível for A largura da viga é de 8 metros.
Passo 1
Salve salve galerinha do RespondeAí, tudo belezinha com vocês?
Saca só, nesse exercício aqui o enunciado nos diz que as extremidades da viga de madeira devem ser entalhadas como mostra a figura. Sabendo que a viga tem que suportar o carregamento mostrado, o enunciado nos pede para determinar a menor profundidade da viga no entalhe se a tensão de cisalhamento admissível for e a largura da viga for metros.
A melhor forma de começar a questão é calculando as reações de apoio na viga:
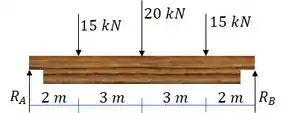
Como o carregamento e as reações são simétricos:
Pelo somatório de forças:
Logo:
Passo 2
Agora calculamos o momento de inércia da região com entalhe. Abaixo tem um desenho da seção:
Esta é uma seção retangular, então o momento de inércia será:
Por enquanto não vamos aplicar valores. Vamos pro próximo passo.
Passo 3
A gente quer calcular a resistência da viga. Então vamos ter que calcular a máxima tensão de cisalhamento.
Pra isso, vamos ter que considerar o momento estático máximo! No desenho, a região do momento estático máximo está destacada em laranja:
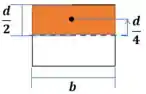
O momento estático é calculado multiplicando a área pelo centroide:
Logo:
Passo 4
Até aqui tudo certo! Agora vamos considerar o cisalhamento máximo na figura.
Aplicamos a equação do cisalhamento:
Vamos substituir as expressões de e que já calculamos:
E com um pouco de matemágica, vamos simplificar a expressão:
Perfeito!
Mas o nosso objetivo é o , então vamos isolá-lo:
E pra terminar a questão, vamos aplicar os valores conhecidos, e e :
Logo, vamos obter que:
Passo 5
O resultado pode parecer estranho, mas esta questão contém um erro de tradução! Na versão original do livro, a tensão admissível é e a largura da viga é . E com esses valores, o resultado final seria: .