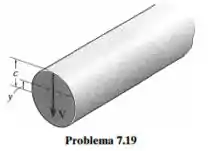
Faça uma representação gráfica da distribuição da tensão de cisalhamento na seção transversal de uma haste com raio c. Quantas vezes a tensão de cisalhamento máxima é maior que a tensão de cisalhamento média que age na seção transversal?

Então vamos começar calculando o momento de inércia, pois este é um valor constante.

E a área da circunferência é

Agora vamos fazer uma função que represente o momento estático.

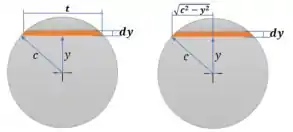
Primeiro vamos imaginar uma seção sobre a circunferência, de espessura infinitesimal , a uma distância do centro e de base .

Podemos usar o teorema de pitágoras para determinar em função de e .

Com isso, podemos determinar o momento estático como uma soma do momento estático dessas “tiras” infinitesimais, isso é expresso pela integral da equação 7.2 do livro texto.

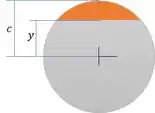
Vamos determinar a área de uma “tira” como:

Vamos substituir o valor da área na integral. Para gerar uma função para o momento estático integramos a partir de um ponto qualquer até atingir o raio .

Efetuando a integral:

Chegamos na expressão:

NOTA: a integral se dá de “ à c” e não ao contrário. Pois observe que o sentido de crescimento de é do centro até o tamanho do raio

Agora aplicamos isso na equação 7.3

Chegamos a uma função que representa a tensão em qualquer ponto da seção circular.

Para encontrar a tensão máxima vamos derivar a equação e igualar a zero:

Então o ponto onde a tensão é máxima é:

Aplicando na equação:

Para calcular a tensão de cisalhamento média utilizamos a equação geral da tensão:

Concluímos a questão dividindo as tensões uma pela outra