Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 56

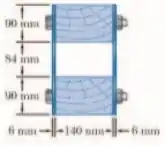
Uma viga composta é feita unindo-se as partes de madeira e aço com parafusos de 12 mm de diâmetro espaçados longitudinalmente a cada 200 mm. O módulo de elasticidade é de 10 GPa para a madeira e 200 GPa para o aço. Para uma força cortante vertical de 4 kN, determine (a) a tensão de cisalhamento média nos parafusos e (b) a tensão de cisalhamento no centro da seção transversal.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

Deixe o aço ser o material de referência.

n s = 1,0 n w = E w E s = 10 G P a 200 G P a = 0,05

Profundidade da seção: d = 90 + 84 + 90 = 264   m m

Para porção de aço, I s = 2 1 12 b d 3 = 2 1 12 6 264 3 = 18,400 × 10 6   m m 4

Para a porção de madeira,

I w = 1 12 b d 1 3 - d 2 3 = 1 12 140 264 3 - 84 3 = 207,75 × 10 6   m m 4

Para a seção transformada,

I = n s I s + n w I w

I = 1,0 18,400 × 10 + 0,05 207,75 × 10 6 = 28,787 × 10 6 m m ³

Passo 2

(a) Tensão de cisalhamento nos parafusos.

Para a parte superior de madeira,

Q w = 90 140 42 + 45 = 1,0962 × 10 6 m m ³

Para a parte transformada de madeira,

Q = n w Q w = 0,05 1,0962 × 10 6 = 54,81 × 10 6 m m 3 = 54,81 × 10 - 6 m ³

Fluxo de cisalhamento na parte superior da madeira:

q = V Q I = 4000 54,81 × 10 - 6 28,787 × 10 - 6 = 7616   N / m

F = q s = 7616 0,200 = 1523,2   N

A b o l t = π 4 d b o l t 2 = π 4 12 2 = 113,1 m m 2 = 113,1 × 10 - 6 m ²

Cisalhamento duplo:

τ = F b o l t 2 A b o l t = 1523,2 2 113,1 × 10 - 6 = 6,73 × 10 6 P a = 6,73   M P a

Passo 3

Para duas placas de aço,

Q = 2 6 90 + 42 90 - 42 = 76,032 × 10 3 m m 3 = 76,032 × 10 - 6 m ³

Para o eixo neutro,

Q = 54,81 × 10 - 6 + 76,032 × 10 - 6 = 130,842 × 10 - 6 m ³

Fluxo de cisalhamento através do eixo neutro:

q = V Q I = 4000 130,842 × 10 - 6 28,787 × 10 - 6 = 18,181 × 10 3 N / m

Espessura dupla:

2 t = 12 m m = 0,012 m

Tensão de cisalhamento:

τ = q 2 t = 18,181 × 10 3 0,012 = 1,515 × 10 6 P a

τ = 1,515   M p a

Resposta

(a) τ = 6,73   M P a ;

(b) τ = 1,515   M p a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma viga extrudada, com a seção transversal mostrada, determinar:A distribuição de tensões de cisalhamento, causando pela força cortante vertical V, aplicada em O.
Para uma viga extrudada, com a seção transversal mostrada, determinar:A localização do centro de cisalhamento O.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a 3 m m . Para uma força cortante vertical de 10 k N , determinar:A tensão de cisalhamento no ponto A
Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a 3 m m . Para uma força cortante vertical de 10 k N , determinar:A máxima tensão de cisalhamento na