Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 22

A viga está sujeita a uma carga uniforme w. Determine a localização a dos apoios de modo que a tensão de cisalhamento na viga seja a menor possível. Qual é essa tensão?

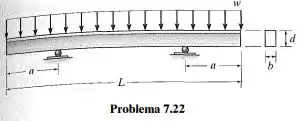
Passo 1

Começamos calculando as reações de apoio:

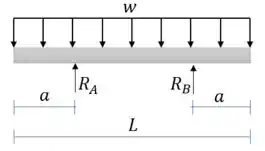
Como o carregamento distribuído é perfeitamente simétrico e as reações também são simétricas:

R A = R B = w L 2

Passo 2

Agora podemos utilizar o método das áreas para gerar o gráfico de esforço cortante:

A a z u l = a ⋅ w

A l a r a n j a = w ( L - 2 a )

Aplicando no gráfico:

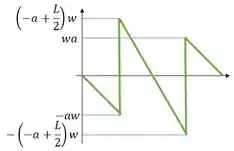
Passo 3

O nosso objetivo é dar um valor para a de forma que a tensão seja a menor possível. Para que isso aconteça, temos que minimizar o esforço cortante.

Então observe o gráfico de esforço cortante. Perceba que ele possui 4 pontos de máximo: A ,   B ,   B ' e A ' .

Se o valor de a for pequeno, os picos B e B’ serão grandes e os A e A’ serão pequenos. Se o valor de a for grande, então A e A’ serão grandes e B e B’ serão pequenos.

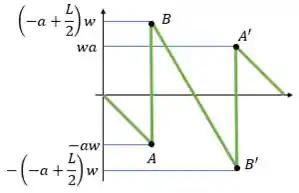
Então, a melhor forma de minimizar a força cortante é fazer com que todos os picos tenham a mesma intensidade.

a w = L 2 - a w

Resolvendo:

a = L 2 - a

2 a = L 2

Assim, o valor de a deve ser:

a = L 4

E assim o valor do cisalhamento é:

V = w L 4

Passo 4

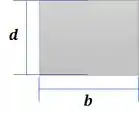
Agora vamos calcular o momento de inércia da seção:

I = b d 3 12

Passo 5

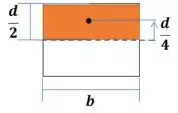
E calculamos o momento estático

Q = b ⋅ d 2 ⋅ d 4

Q = b d 2 8

Passo 6

Concluímos aplicando a equação do cisalhamento

τ = V Q I t

Substituíndo os valores:

τ = a L 4 ⋅ b d 2 8 b d 3 12 ⋅ b

τ = a L 4 ⋅ b d 2 8 ⋅ 12 b d 3 ⋅ b

Chegamos em:

τ = 3 w L 8 b d

Resposta

τ = 3 w L 8 b d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Várias pranchas de madeira são coladas para formar a viga de seção caixão mostrada. Sabendo que a viga está submetida a uma força cortante vertical de 3 kN, determine a tensão de cisalhamento média na
A viga de alumínio extrudado tem uma espessura de parede uniforme de 1 8 i n . Sabendo que o cisalhamento vertical na viga é de 2k i p s , determine a tensão de cisalhamento correspondente em cada um
O projeto de uma viga exige que duas placas retangulares verticais de 1 8 × 4i n . sejam conectadas por soldas a duas placas horizontais com 1 2 × 2i n . conforme mostrado. Para uma força cortante ver
(a)Determine a tensão de cisalhamento no ponto P de um tubo de paredes finas com a seção transversal mostrada na figura. Provocada por uma força cortante vertical V . (b) Mostre que a tensão de cisalh
A viga de madeira mostrada na figura está submetida a uma força cortante vertical de 5,34 kN. Sabendo que a força cortante admissível nos pregos é 333,6 N, determine o maior espaçamento possível s dos