Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 44

Uma viga consiste em três pranchas conectadas por parafusos de aço espaçados longitudinalmente de 225 mm conforme mostrado. Sabendo que a força cortante na viga é vertical e igual a 6 KN e que a tensão de cisalhamento média admissível em cada parafuso é de 60 MPa. Determine o menor diâmetro permissível para os parafusos a serem utilizados.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine o menor diâmetro permissível para os parafusos a serem utilizados. Para isso vamos esboçar o diagrama de corpo livre, vem comigo ;)

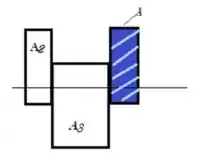
Passo 2

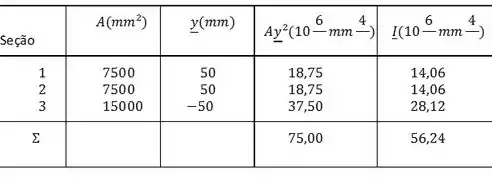
Agora temos que determinar a inércia vem comigo ;)

I = Σ   A y _ ² + Σ I _ = 131,25   x   10 6 m m 4 131,25   x   10 - 6 m 4

Q = A y ¹ _ = 7500 50 = 375   x   10 3 m m 3 = 375   x   10 - 6 m ³

Passo 3

Vamos determinar a área partiu!!

A = V Q s t b o l t I = ( 6   x   10 ³   ) ( 375   x   10 - 6   ) ( 0.225 )   ( 6   x   10   ) ( 131.25 x   10   6 ) = 64,286   x   10 - 6 m 2 = 64,286 m m ² .

Agora sim podemos determinar o diâmetro

d = 4 A b o l t π = ( 4 ) ( 64.286 ) π = 9,05 m m

Resposta

9,05 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga de alumínio extrudada tem a seção transversal mostrada na figura. Sabendo que a força cortante vertical na viga é 150 kN, determine a tensão de cisalhamento no (a) ponto a e (b) ponto b.
Para a viga construída no Prob. 6.1, determine a tensão de cisalhamento admissível se o espaçamento entre cada par de pregos é s = 45 mm
Três pranchas de 50 x 100 mm são pregadas juntas para formar um viga que é submetida a uma força cortante de 1500 N. Sabendo que a tensão de cisalhamento admissível em cada prego é de 400 N, determine
Uma viga caixão quadrada é feita de duas pranchas 20 x 80 mm e duas pranchas de 20 x 120 mm pregadas entre si, como mostrado na figura. Sabendo que o espaçamento entre os pregos é de s= 30 mm e que a
Para a viga e carregamento mostrado, considere a seção n-n e determinar (a) o maior tensão de cisalhamento nessa seção, (b) a tensão de cisalhamento ponto a.