Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 103
Um fazendeiro de tenta evitar a vaca escape enrolando a corda com duas voltas em torno do tronco da árvore, como mostra a figura. Se a vaca exerce uma forca de sobre a corda, determine se o fazendeiro conseguirá evitar a fuga da vaca. O coeficiente de atrito estático entre a corda e o tronco da árvore é , e entre as botas do fazendeiro e o solo é .
Passo 1
Falaaa, querido! A gente quer saber se o fazendeiro consegue segurar a vaquinha. Para isso, precisamos ver se o atrito nos pés dele considerando que ele está numa situação de equilíbrio é maior ou menor que o atrito máximo estático, dado por
Primeiro vamos achar a força de tração exercida pelo fazendeiro. Para isso vamos usar o seguinte:
é a força que visa vencer e o atrito, é a força que está na direção do movimento. Quem tá tentando se mover? Isso mesmo! A vaquinha! Então .
é a força que está “ajundando” o atrito a deixar o sistema parado. Então é a força exercida pelo fazendeiro, a que queremos achar.
Além disso, o ângulo é o ângulo da superfície de contato entre a corda e o tronco da árvore. Como ele deu duas voltas completas, temos:
E é coeficiente de atrito entre o tronco e a corda. Substituindo nossos dados:
Assim,
Passo 2
Agora vamos analisar o fazendeiro. Olha esse DCL:
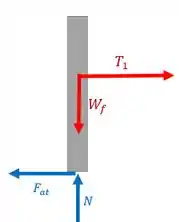
A reação da corda é puxa-lo para a direita e a força de atrito fica no sentido oposto. A gente também não pode esquecer que ele tem uma massa de .
Como ele está em equilíbrio, temos:
Assim,
Para o eixo :
Então,
Passo 3
Pra finalizar, vamos comparar a força de atrito com .
Percebe que
Como a força de atrito máxima é bem maior que a força de atrito necessária para manter o fazendeiro parado no nosso sisteminha em equilíbrio, ele está paradinho e deve conseguir conter a vaquinha sim. 😊
Resposta
O fazendeiro consegue evitar a fulga da vaca.