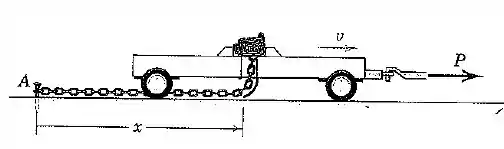
O carrinho transporta uma pilha de uma corrente de elos com massa por unidade de comprimento. A corrente passa livremente através do orifício no carrinho e é conduzida ao repouso, elo por elo, pela tração na porção da corrente que repousa sobre o solo e está presa em sua extremidade . O carrinho e a corrente sobre ele se deslocam sob a ação da força constante e possuem velocidade e massa quando . Determine as expressões para a aceleração e a velocidade do carrinho em termos de se todo o atrito é desprezado. Encontre também . Observe que o elo de transição é desacelerado da velocidade para a velocidade nula pela tração transmitida pelo último elo horizontal . Observe também que o elo não exerce nenhuma força sobre o elo seguinte durante a transição. Explique por que o termo está ausente se a é aplicada a esse problema.

Nossa próxima tarefa é encontar a velocidade em função da posição. Podemos fazer isso reescrevendo a aceleração desse jeito:

E substituindo a nossa fórmula para a aceleração:

E ficamos com uma equação diferencial separável que pode ser resolvido para acharmos a nossa função:

E agora odemos isolar a velocidade:

Agora só falta encontrar a tração na corrente. Podemos pensar que age como uma força para o “escoamento” da corrente, em que a taxa de escoamento de massa é:

E a força “imprime” a seguinte variação de velocidade:

Mas como a tração é a mesma em todos os pontos da corrente, apontando em mais de uma direção, faz sentido tratar apenas do seu módulo:

A equação que o enunciado menciona é a seguinte:

O termo está associado à força produzida pelas partículas que deixam um certo corpo sobre o próprio corpo. Pense por exemplo no combustível que sai de um foguete, e exerce uma força sobre ele ao fazer isso.

Nesse caso, segundo o próprio enunciado, a corrente “passa livremente através do orifício do carrinho”, então é de se esperar que esse termo seja nulo.