Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 155

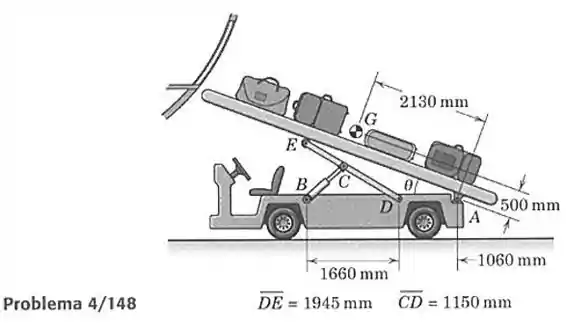
148- A máquina mostrada é usada para ajudar a carregar bagagens em aviões. A massa combinada da esteira e das bagagens é de 100   k g , com um centro de massa em G . Determine a força no cilindro hidráulico, faça seu gráfico em função de θ na faixa 5 ≤ θ ≤ 30 , e calcule seu valor máximo nessa faixa.

Passo 1

Precisamos dois diagramas de forças para resolver esse exercício, o sistema de forças na esteira e no eixo que contém o cilindro hidráulico B C .

Começando pelo eixo E C D , temos as seguintes forças.

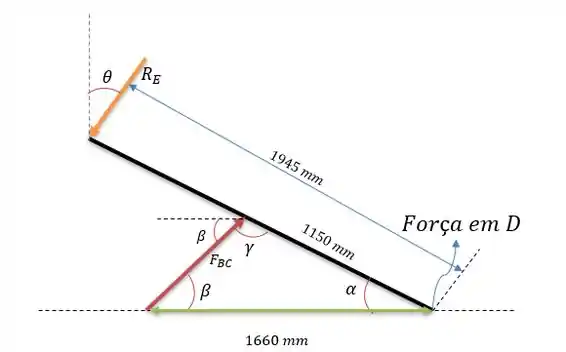
Onde a esteira imprime uma reação em E normal a sua angulação θ .

Agora na esteira.

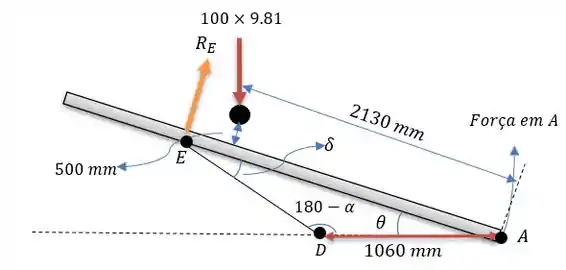
Passo 2

Na segunda imagem se aplicarmos lei dos senos conseguimos encontrar α :

sin ⁡ θ D E = sin ⁡ ( 180 - α ) A E

sin ⁡ 180 - α = A E D E sin ⁡ θ

O valor de δ será:

sin ⁡ θ 1.945 = sin ⁡ δ 1.06

δ = sin - 1 ⁡ 0.545 sin ⁡ θ

Logo o valor de α será:

180 - α + θ + δ = 180

α = θ + γ

Antes de encontrar os valores de γ e β precisamos do valor do comprimento da reta B C , isso se encontra pela lei dos cossenos, o mesmo raciocínio pode ser aplicado para encontrar o valor de comprimento da reta A E .

Lei dos cossenos para encontrar o valor de B C .

B C 2 = B D 2 + C D 2 - 2 B D C D cos ⁡ α

B C = 1.660 2 + 1.15 2 - 2 × 1.66 × 1.15 cos ⁡ α

B C = 4.0781 - 3.818 cos ⁡ α

Logo os valores de γ e β serão:

sin ⁡ α B C = sin ⁡ γ 1.66 = sin ⁡ β 1.15

β = sin - 1 ⁡ 1.15 × sin ⁡ α B C

γ = sin - 1 ⁡ 1.66 × sin ⁡ α B C

Pela lei dos cossenos temos o valor de A E .

A E 2 = 1.945 2 + 1.06 2 - 2 × 1.945 × 1.06 × c o s ⁡ ( 180 - α )

A E = 4.9066 - 4.1234 cos ⁡ ( 180 - α )

Passo 3

Agora podemos partir para o cálculo das forças, para isso vamos fazer primeiro a somatória dos momentos em A na esteira para sermos capazes de descobrir a força R E .

R E × A E - 100 × 9.81 × 2.13 cos ⁡ θ + 100 × 9.81 × 0.5 sin ⁡ θ = 0

R E × A E = 2089.53 cos ⁡ θ - 490.5 sin ⁡ θ

R E = 2089.53 cos ⁡ θ - 490.5 sin ⁡ θ A E

Agora para o eixo vamos fazer a somatória dos momentos em D .

- R E cos ⁡ θ × E D c o s   α - R E sin ⁡ θ × E D s i n   α + F B C sin ⁡ γ × 1.15 = 0

F B C = R E × 1.945 × cos ⁡ θ cos ⁡ α + s i n θ sin ⁡ α 1.15 sin ⁡ β

Resposta

Gráfico de F B C :

E .

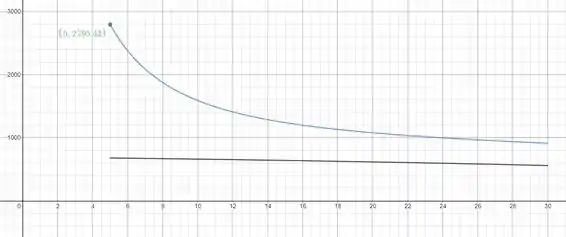
Link do gráfico: https://www.desmos.com/calculator/utaouhqe65

F m a x B C = 2795.43   N   e m   θ = 5 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força (magnitude e direção) que o membro B C exerce no membro A B ( a ) se a carga 900N for aplicada ao centro do membro A B , e ( b ) se a carga 900N for aplicada ao centro do membro B C
Determine os componentes de todas as forças que atuam em cada membro da estrutura carregada.
Determine a magnitude da reação do pino em B ( a ) ignorando o fato de que B D é um membro de duas forças e ( b ) reconhecendo o fato de que B D é um membro de duas forças.
Para qual valor M do binário no sentido horário o componente horizontal A x da reação do pino em A será zero? Se um binário da mesma magnitude M fosse aplicado no sentido anti-horário, qual seria o va
O macaco do pára-choque do automóvel é projetado para suportar uma carga descendente de 4000N . Comece com um diagrama de corpo livre de B C D e determine a força suportada pelo rolo C . Observe que o