Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 06
Determine a magnitude e a direção da força de atrito que a parede vertical exerce no bloco de se e .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o módulo e a direção da força de atrito que a superfície vertical da parede causa no bloco para duas situações: e .
Então bora resolver! Vamos começar analisando o diagrama de corpo livre do sistema:
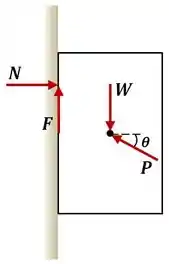
Onde:
E os coeficientes de atrito:
Estamos considerando que a força de atrito aponta para cima e a normal para a direita, caso em nossos cálculos a gente encontre valores negativos de e , significa que na verdade eles estão com orientações contrárias a essas.
Passo 2
Vamos começar então pela situação . Assumindo a condição de que a estrutura está em repouso, podemos utilizar as equações de equilíbrio de forças nas direções e para determinar a reação normal de contato e a força de atrito exercidas pela superfície vertical na caixa.
Passo 3
Tranquilinho né? Temos ainda que para o corpo na condição de equilíbrio, a força de atrito máxima () é dada pelo produto entre a reação normal e o coeficiente de atrito estático:
Uma vez que:
Logo, nossa hipótese não é válida, o corpo está em movimento e a força de atrito é dada por:
Passo 4
Agora ficou fácil né? Vamos repetir os mesmos cálculos para a situação
Novamente, assumindo que a estrutura está em repouso, vamos utilizar as equações de equilíbrio de forças nas direções e para determinar e .
Passo 5
Show de bola! Calculando a força de atrito máxima () para essa condição:
Uma vez que:
Nossa hipótese é válida, o corpo está em repouso com .
Essa foi de boa hein?
Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 