Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 148
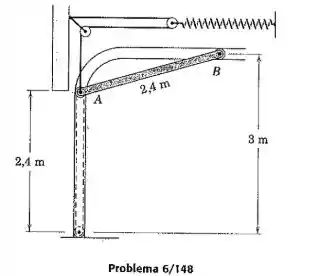
A figura mostra a seção transversal de uma porta de garagem de , que é um painel retangular uniforme de por . A porta movimenta dois conjuntos de molas, um em cada lado da porta, tal como apresentado. Cada mola possui uma rigidez de e está sem deformação quando a porta está na posição aberta indicada. Se a porta é liberada a partir do repouso nessa posição, calcule a velocidade da extremidade em , quando atinge o piso da garagem.
Passo 1
Para a resolução deste problema aplicaremos a equação de Trabalho-Energia:
,
Em que, por definição, representa o trabalho de todas as forças externas além das forças gravitacionais e de molas. Neste caso, portanto, .
Passo 2
A variação da energia cinética do corpo é dada por
Para a variação de energia potencial, temos
,
em que e
Note que, neste exercício, a força que age sobre é . Assim sendo, quando o ponto percorre na vertical, a extremidade da mola ligada à polia percorre na horizontal. Logo, a variação da energia potencial elástica é dada por
Já a variação da energia potencial gravitacional fica
Passo 3
Retomando a equação Trabalho-Energia e substituindo as equações encontradas:
Resolvendo para , ficamos com