Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 152

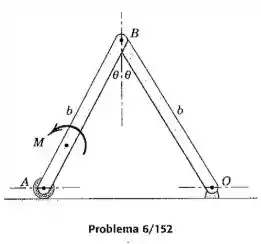
As duas barras esbeltas cada uma de massa m e comprimento b estão unidas por um pino e se deslocam no plano vertical. Se as barras são liberadas a partir do repouso na posição mostrada e se deslocam juntas sob a ação do momento M de módulo constante aplicado a A B , determine a velocidade de A quando atingir O .

Passo 1

A variação da energia cinética é dada por

∆ V = ∆ V g +   ∆ V e

Por não haver deformação elástica, o termo temos ∆ V e = 0 . Assim,

∆ V = ∆ V g = 2 × m g b 2 - b 2 c o s θ = m g b ( 1 - c o s θ )

Note que a barra BO está fixa pelo ponto O e, portanto, rotaciona em torno dele. Assim,

∆ T B O = 1 2 I o ω 2 = 1 2 1 3 m b 2 v b b 2 = 1 6 m v b ²

Observe que conforme θ → 0 , v b → 1 2 v A . Realizando essa substituição na equação anterior, temos

∆ T B O = 1 6 m 1 4 v A ² = 1 24 m v A ²

Partindo de análise semelhante, concluimos que a barra AB gira em torno de C, de forma que

∆ T A B = 1 2 I c ω 2 = 1 2 1 12 m b 2 + m 3 b 2 2 v A 2 b 2

∆ T A B = 7 24 m v A ²

Passo 2

Aplicando a relação Trabalho-Energia, temos que

U ' = ∆ T + ∆ V

Sabemos também que para rotações finitas e momento constante,

U ' = M θ

Substituindo os valores encontrados no passo anterior, ficamos com:

M θ =   1 24 m v A 2 + 7 24 m v A 2 + m g b ( 1 - c o s θ )

Simplificando m e isolando v A , achamos

v A = 3 M θ m - g b ( 1 - c o s θ

Resposta

v A = 3 M θ m - g b ( 1 - c o s θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de 5 kg é fixado a uma mola indeformada de constante k = 2.100 N/mm. Os coeficientes de atrito estático e cinético entre o bloco e o plano são0,60 e 0,40 , respectivamente. Se a força F é len
Um bloco de 5 kg é fixado a uma mola indeformada de constante k = 2.100 N/mm. Os coeficientes de atrito estático e cinético entre o bloco e o plano são 0,60 e 0,40 respectivamente. Se a força F é lent
Um colar C de 4 kg desliza sobre uma barra horizontal entre as molas A e B. Se o colar é empurrado para a direita até que a mola B seja comprimida 50 mm e em seguida liberada, determine a distância qu
Dois blocos A e B, de massa de 4 kg e 5 kg, respectivamente, estão conectados por uma corda que passa pelas roldanas do modo mostrado na figura. Um colar C de 3 kg é colocado sobre o bloco A e o siste
Quatro pacotes de 3 kg são mantidos no lugar por atrito sobre uma correia transportadora que está desengatada de seu motor de acionamento. Quando o sistema é liberado do repouso, o pacote 1 deixa a es