Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 48
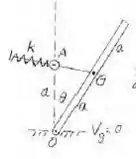
A figura mostra a vista lateral OA de uma porta de ventilador uniforme de massa m que fecha a abertura OC em uma parede vertical. A mola de rigidez k é descomprimida quando θ = 0, e a haste de luz que a confina passa pelo colar pivotado C. Com este projeto, mostre que a porta permanecerá em equilíbrio para qualquer ângulo θ se a mola tiver a rigidez k adequada.
Passo 1
O enunciado pede que a gente mostre que a porta permanecerá em equilíbrio para qualquer ângulo θ se a mola tiver a rigidez k adequada.
Passo 2
Resposta
Exercícios de Livros Relacionados
6. O mecanismo articulado de duas barras mostrado na figura é sustentado por um pino e um suporte em B e por um colar em D , que desliza livremente sobre uma haste vertical. Determine a força P necess
7. Uma mola de constante 15N / c m é presa a pinos nos pontos C e F tal como mostra a figura. Desprezando o peso da mola e do mecanismo articulado, determine a força na mola e o deslocamento vertical
14. Deduza uma expressão para a intensidade da força Q necessária para manter o equilíbrio do mecanismo mostrado na figura.
10. Resolva o Problema 10.9 considerando que a força P aplicada no ponto A atua horizontalmente para a esquerda.
3. Determine o binário M que deve ser aplicado ao elemento A B C para se manter o equilíbrio do sistema articulado.