A figura representa uma peça plana de uma chapa metálica, simétrica em relação ao eixo A-A e que tem o contorno superior parabólico. Escolha as suas próprias coordenadas e calcule a distância a partir da base até o centro de gravidade da peça
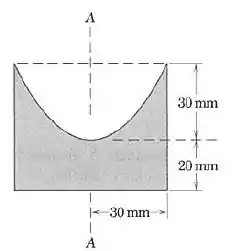
Passo 1
Sabendo que a equação para encontrar o centroide é dado por:
Dessa maneira, vamos primeiro encontrar a área do problema.
Passo 2
Mas antes vamos escolher um elemento de área, para assim podermos integrar, bem como nossa origem de coordenadas, com isso:
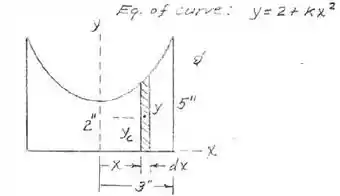
Pronto! Escolhido o elemento de área vamos integrar ele em relação a x e temos a nossa área. Como também, por simetria podemos utilizar metade da área para facilitar os cálculos. Dessa maneira:
Mas antes precisamos encontrar a função que descreve esta parábola. Sabendo que a equação que descreve uma parábola é dada por:
Note que, quando o x=0 temos .
Logo,
Sendo que, quando x = 30, teremos:
Com isso:
Passo 3
Tendo a função que descreve o nosso problema fica mais fácil de integrar, dessa maneira a área é dada por:
Agora basta resolvermos essa integral que teremos nossa área, sendo que:
Passo 4
Vamos encontrar o centroide em relação a coordenada y.
Mas antes de aplicar a equação para achar o centroide na coordenada y, vamos resolver a integral:
Depois é só dividir pela área que teremos o ponto.
Cuidado! Para encontrarmos o centroide em relação a y, teremos que ter um cuidado, o ponto Y na nossa delimitação da área está no meio dos extremos, ou seja,
Lembre-se que o dA também é dado por:
Com isso,
Logo,
Dessa maneira:
Passo 5
Agora substituindo na equação do centroide, temos: