Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 137
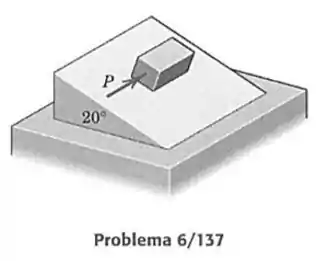
137- O bloco de está em repouso sobre o plano inclinado a , com um coeficiente de atrito estático . Determine a força horizontal mínima que fará com que o bloco deslize.
Passo 1
Da forma como está mostrado o bloco tenderá a descer a rampa e ir para a direita ao mesmo tempo, tendo atrito nos eixos que estão paralelas ao plano, uma por causa do peso do bloco e outra por conta da força que tende a empurrar a mesma para a direita (pelo nosso referencial).
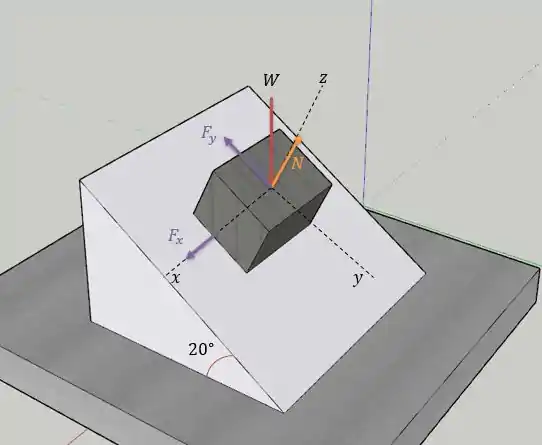
Passo 2
A força peso do bloco não pode ser rebatida em somente em e então fazendo o diagrama de corpo livre do bloco nos eixos nós teremos:
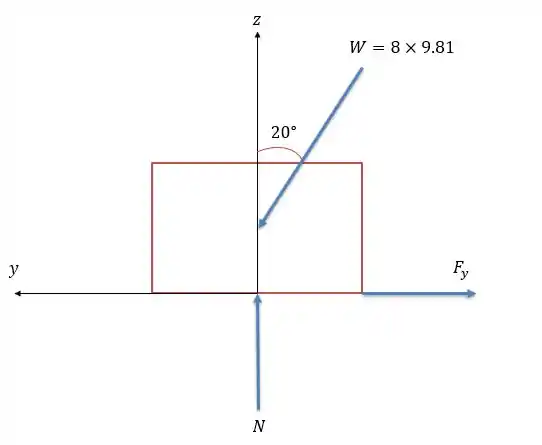
Onde a força peso acaba aparecendo de forma inclinada pois os nossos eixos no bloco estão normais ao plano inclinado.
Agora nos eixos
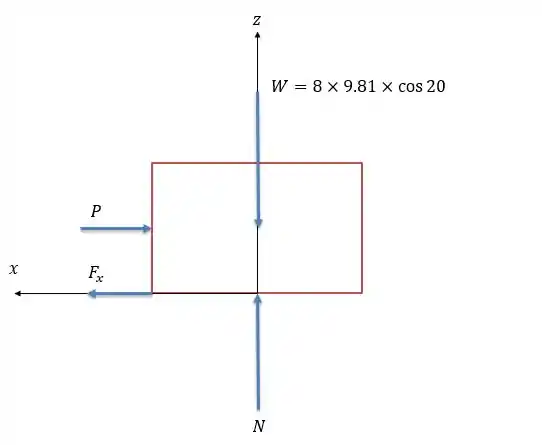
Como não podemos projetar o peso no eixo (ela é uma força que está nos eixos e somente) o nosso sistema fica somente com a componente no eixo .
Passo 3
Nos dois sistemas podemos dizer que a componente normal será igual a (pela somatória das forças horizontais):
Essa força normal é composta por duas componentes de atrito e e seus valores devem ser calculadas separadamente em suas respectivas visões.
Agora fazendo a somatória das forças horizontais nos eixos podemos achar o valor de :
Pela somatória das forças horizontais podemos calcular como:
A força de atrito total pode ser calculada da seguinte forma:
E essas duas forças que comporão a força normal:
Como teremos:
Calculando :