Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 135
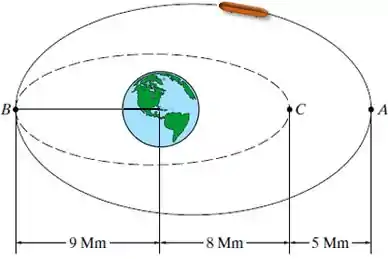
O foguete está em uma órbita elíptica de voo livre em torno da Terra de tal maneira que , como mostrado. Determine sua velocidade escalar quando ele está no ponto . Também determine a variação súbita na velocidade escalar que o foguete tem que passar em a fim de se mover em voo livre ao longo da órbita indicada pela trajetória pontilhada.
Passo 1
O encunciado nos dá a seguinte informação:
Órbita elíptica com excentricidade .
Devemos determinar a velocidade escalar do foguete no ponto e a variação de velocidade sofrida ao passar em , para que sua órbita seja alterada para uma segunda trajetória elíptica que agora passará pelo ponto .
Suponha que o raio da Terra é 6378 km;
A massa da Terra é de 5,976(1024) kg;
A massa do Sol é de ,99(1030) kg;
A constante gravitacional é de .
Raio da Terra:
Passo 2
Sabemos que a excentricidade é igual a
Onde as constantes e são definidas por
Substituindo e na equação da excentricidade e colocando em evidência, obtemos
Substituindo os valores de e para a primeira trajetória, temos que
Onde .
Como é uma constante, podemos utilizar a seguinte relação para encontrar :
logo,
Passo 3
Agora vamos analisar a segunda trajetória.
Nesta nova trajetória, , , e .
Primeiramente, vamos encontrar a excentricidade . Sabemos que
Porém, não sabemos a velocidade no ponto .
Sabemos que, em uma trajetória elíptica, a seguinte relação é verdadeira:
Relacionando ambas as equações citadas, obtemos
Substituindo os valore de e , podemos encontrar :
Passo 4
Em seguida, vamos encontrar
Como é uma constante, podemos utilizar a seguinte relação para encontrar :
logo,
Passo 5
Portanto, a variação em será de
Ou seja, a velocidade irá diminuir para que o foguete consiga sair da primeira trajetória elíptica e entre na órbita pontilhada.