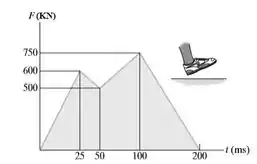
O gráfico mostra a força reativa vertical entre solo e sapato como uma função do tempo, onde o primeiro pico representa a força reativa com relação ao calcanhar e o segundo com relação à parte frontal do pé. Calcular o impulso total envolvido durante a interação.
Passo 1
Sabemos que:
Portanto, o impulso será a área abaixo da curva que representa a força F em função do tempo. Por isso podemos calcular a área formada pela interação da força entre o sapato e o solo, ao longo do tempo.
Passo 2
Sabendo isso, podemos calcular as áreas das formas geométricas 1, 2, 3 e 4, demonstradas abaixo:

Logo teremos que:
Com isso:
Resposta
O impulso total gerado pela interação entre o sapato e o solo é de 90KN.s.