Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 21

Uma força de 200   N é aplicada em um suporte ABC como mostrado na figura. Determine o momento da força sobre A.

Passo 1

Desenhando o diagrama do corpo livre:

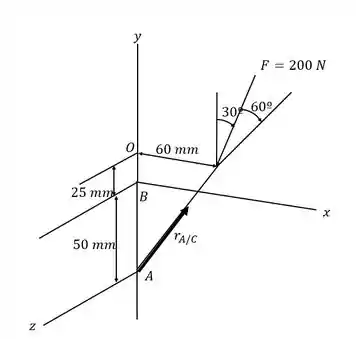
Passo 2

Vamos começar calculando o vetor força:

F = F x i + F y j + F Z k

Substituindo os valores de F x ,   F y   e   F z :

F x = 0

F y = - F c o s θ y = - 200 ⋅ cos ⁡ 30 º = - 173,21   N F   Z = F c o s θ = 200 ⋅ cos ⁡ 60 º = 100   N

F = F x i + F y j + F z k = 0 i + - 173,21 j + ( 100 ) k

Passo 3

Escrevendo as coordenadas dos pontos:

O = 0,0 , 0 A = 0 , - 0,075,0   m C = 0,06,0 , 0   m

Passo 4

Calculando a posição do vetor r A C usando a equação:

r A / C = A C = O C - O A x c - x 0 i + y c - y 0 j + z c - z 0 k - x A - x 0 i + y A - y 0 j + z A - z 0 k

Substituindo:

r A C =   0,06 - 0 i + 0 - 0 j + 0 - 0 k - 0 - 0 i + - 0,075 - 0 j + 0 - 0 k r A C = 0,06 i - - 0,075 j + 0 k r A C = 0,06 i + 0,075   j + 0 k

Passo 5

Calculando o momento da força sobre A como se segue:

M A = r A C × F

M A = 0,06 i + 0,075   j + 0 k × ( 0 i - 173,21 j + 100 k )

M A = i j k 0,06 0,075 0 0 - 173,21 100 = = 0,075 × 100 i + 0,06 × - 173,21 k + 0 - 0 + 0 + 100 × 0,06 × k = 7,5 i - 6 j - 10,39 k   N ⋅ m  

Resposta

M A = 7,5 i - 6 j - 10,39 k   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

131. A montagem mostrada na figura consiste em uma barra A F de 80m m que é soldada a uma cruz representada por quatro braços de 200m m . A montagem é mantida por uma rótula em F e por três conexões c
136. Resolva o Problema 4.135 , considerando que o arame C E é substituído por um arame que conecte E e D .
139. Resolva o Problema 4.138 , sujeito à restrição de que H deve estar sobre o eixo y .
137. Duas placas retangulares são soldadas juntas para formar o conjunto mostrado na figura. O conjunto é sustentado por rótulas em B e D e por uma esfera sobre uma superfície horizontal em C . Para o
140. O tubo A C D E é suportado por rótulas em A e E e pelo arame D F . Determine a tração no arame quando a carga de 640N é aplicada em B como mostrado na figura.