Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 133

Uma força de é aplicada à alça do guincho, conforme mostrado. A força encontra-se em um plano paralelo ao plano - e perpendicular à linha da alça. Determine os momentos desta força sobre o ponto O e sobre o eixo .

Passo 1

Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!

O enunciado nos pede duas coisas:

i) Determinar o momento da força de sobre o ponto O ();

ii) Determinar o momento da força de sobre o eixo ().

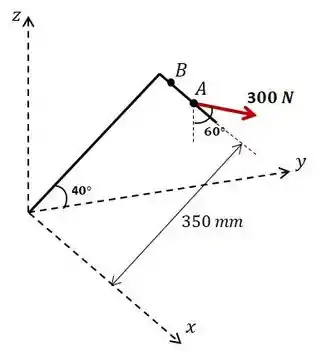
Show, então bora lá! Pra gente calcular o momento exercido pela força sobre o ponto O precisamos, primeiro, definir a força na forma vetorial e o vetor distância do ponto A de aplicação da força até o ponto O. Calma que é bem tranquilo!

Para decompor a força, temos que lembrar que ela está sendo aplicada em um plano paralelo ao plano - e, portanto, só tem componentes nas direções e . Fazendo então a projeção da força de nesses eixos, temos:

Passo 2

O próximo passo é calcular o vetor distância do ponto de aplicação da força até O, aqui só precisamos somar vetorialmente cada um dos segmentos que ligam o ponto O ao ponto A, sem esquecer de decompor a reta nos eixos , e :

Boa! Agora temos tudo que precisamos para calcular o momento sobre o ponto O:

Passo 3

Show de bola! Agora só falta o momento sobre o eixo (). Para isso, podemos utilizar a Eq. 2/16:

Mas aqui tem o pulo do gato!! Uma vez que estamos procurando o momento em torno de um eixo cartesiano (eixo ), podemos apenas calcular a projeção de nesse eixo, que é dado pela componente de .