Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 4

A força de 300 N é aplicada em A como mostrado na figura. Determine (a) o momento da força de 300 N sobre D, (b) a intensidade e sentido da força horizontal aplicada em C que cria o mesmo momento sobre D, (c) menor força aplicada em C que cria o mesmo momento e D.

Passo 1

Diagrama do corpo livre:

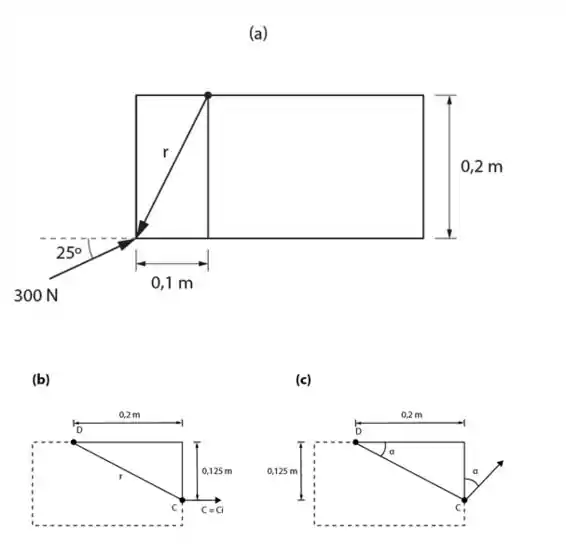
Passo 2

  1. Achando a posição do vetor de D até A:

    2. r A / D = - 0,1   m i + - 0,2   m j

    Achando o vetor força F:

    F = F [ cos ⁡ α i + sen ⁡ α j ]

    Substituindo F e α = 25 º :

    F = 300 [ cos ⁡ 25 ° i + sen ⁡ 25 ° j ] = 271,89   N i + 126,79 N ) j

    Passo 3

    Achando o momento M D   da força F   sobre D :

    M D = r A / D × F

    M D = - 0,1 M i + - 0,2 m j × 271,89 N i + 126,79   N j = - 12,68   N ⋅ m k + 54,38   N ⋅ m k = 41,7   N ⋅ m k

    Passo 4

  2. Agora vamos achar a força agindo em C usando a seguinte expressão:

    3. M D = F C × ( d i s t â n c i a   p e r p e d i c u l a r   e n t r e   D   e   C )

    F C = M D d i s t â n c i a   p e r p e d i c u l a r   e n t r e   D   e   C F c = 41,7   N ⋅ m 0,125   m = 333,6   N

    F C = 333,6   N i ^

    Passo 5

  3. Devemos achar o menor valor de P que acontece quando a distancia perpendicular do ponto C até a linha de ação da força é máxima. Achando a distâcia d da figura para esse caso:

d = 0,2   m 2 + 0,125 m 2 = 0,236   m

d é a distâcia perpendicular do ponto C até o ponto D

Achando o menor valor de P em C usando a expressão:

P = 41,7   N ⋅ m 0,236   m = 176,7   N

Achando o ângulo feito com a vertical:

tan ⁡ θ = 0,2   m 0,125   m   θ = arctan ⁡ 0,2   m 0,125   m = 58,0 º

Portanto menor valor da força é 176,7   N   ∡ 58 º   v e r t i c a l m e n t e

Resposta

M D → = 41,7   N ⋅ m k  

F C → = 333,6   N i ^

F C = 176,7   N   ∡ 58 º   v e r t i c a l m e n t e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove a identidade do produto triplo escalar A * B xx C = A xx B * C .
Se θ = 45 ° , determine o momento produzido pela força de 4k N em relação ao ponto A .
Dois garotos empurram o portão como mostrado. Se o garoto em B exerce uma força F B = 150N , determine a intensidade da força F A que o garoto em A precisa exercer para impedir que o portão gire. Desp
As pinças são usadas para prender as extremidades do tubo de perfuração P . Se um torque (momento) M P = 1200N ∙ m é necessário em P para girar o tubo, determine a força que precisa ser aplicada no ca
Determine o momento mínimo produzido pela força F em relação ao ponto A . Especifique o ânguloθ ( 0 ° ≤ θ ≤ 180 ° ) .