Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 113
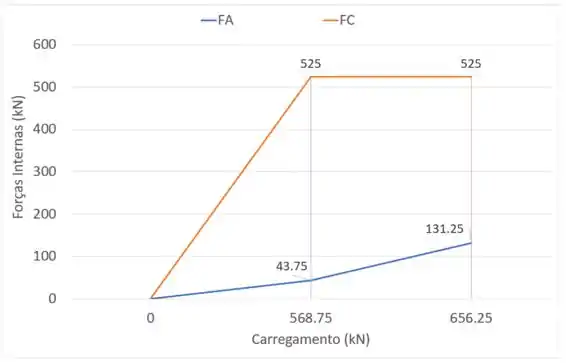
A força é aplicada à barra, a qual é composta por um material elástico perfeitamente plástico. Construa um gráfico para mostrar como a força varia em cada seção e (ordenadas) à medida que (abcissa) aumenta. A barra tem áreas de seção transversal de na região e na região e .
Passo 1
Uma barra horizontal de material elastoplástico está apoiada entre duas paredes. Uma força é aplicada em para direita.
Características da barra:
- Tensão de escoamento:.
- Áreas transversais: , .
- Comprimentos iniciais: , .
- Material elastoplástico.
Precisamos caracterizar o valor das forças internas nas seções e de acordo com , para construir um gráfico! Vamos considerar conhecido.
Primeiro vamos ver como as forças internas ficam no regime elástico. Aí a gente investiga o que acontece quando aumenta muito.
Passo 2
Beleza, no regime elástico é mole! Começamos com equilíbrio de forças. As reações e dos apoios vão resistir o carregamento.
A força é o esforço da seção , que está tracionando. E a força é o esforço em , que está comprimindo.
Precisamos de mais uma equação. Vamos pra compatibilidade.
Passo 3
Vamos pensar com o princípio da superposição. Olhe para o ponto .
- O carregamento puxa a seção para direita, movendo para direita um comprimento .
- A reação empurra a barra toda ( para esquerda, então vai para a esquerda um comprimento
Como o apoio é rígido em (não se move), esses efeitos tem que se anular:
Estamos tratando de regime elástico, então podemos usar relação carga-deslocamento. Atenção para a variação de área!
E retornando ao equilíbrio de forças:
Beleza, pro regime elástico a gente já tem tudo que precisa! Vamos pro regime plástico.
Passo 4
A barra vai entrar em regime plástico quando a tensão em uma das seções ultrapassar . Primeiro passa é descobrir quem alcança isso primeiro.
Bem, a ação da força vai deslocar algum comprimento para direita. Isso vai deformar as seções, comprimindo e esticando o mesmo comprimento! A definição de deformação é pegarmos justamente esse deslocamento e dividirmos pelo tamanho inicial:
Aí que vem a sacada! Perceba que ! Como é o mesmo , temos que sempre
Show! Então a seção sempre escoa primeiro!
Vejamos que valor de faz escoar, e aí vamos aumentando!
Passo 5
A seção vai escoar quando causar tensão . Pela fórmula da tensão:
Isso vai ocorrer quando o carregamento for
Podemos usar relação aqui porque a barra está no limite do regime elástico!
O valor correspondente de será
A força na seção vai permanecer em por causa do comportamento elastoplástico.
Bora, em frente! Vamos aumentar mais o valor de e achar quando a seção também escoa!
Passo 6
A seção vai escoar quando causar tensão . Pela fórmula da tensão:
Não podemos mais usar as relações do Passo 3! Estamos em regime plástico agora! Para achar o correspondente, lembre-se que a força na seção continua sendo (elastoplástico!). Aplique o equilíbrio de forças:
E pronto! Esse é o máximo que a barra consegue aguentar. Se aumentarmos mais o , as forças internas vão continuar como e , não vão balancear , e a barra vai continuar deformando.
Agora é só ser artista e colocar isso tudo em um gráfico!
Passo 7
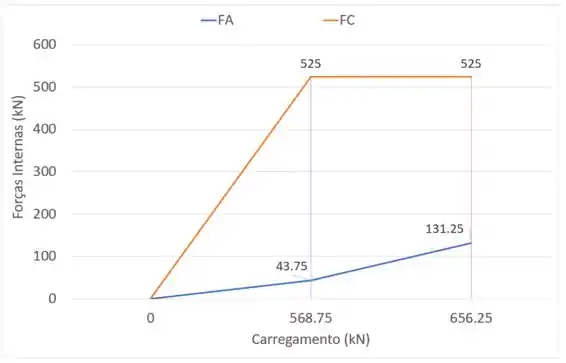
Resposta
