O elo rígido é sustentado por um pino em e dois cabos de aço , cada um com comprimento de quando não alongados e área de seção transversal de . Determine a força desenvolvida nos cabos quando o elo suportar a carga vertical de .
Passo 1
Um elo rígido está apoiado em e ligado a dois cabos: um em e outro em . Uma força vertical de é aplicada.
Características dos cabos:
- Área transversal: .
- Comprimento inicial: .
A força de irá girar o elo em sentido anti-horário ao redor do pino . Isso vai esticar as cordas em e .
As cordas irão resistir a essa tração com forças e .
Queremos descobrir essas forças!
Passo 2
Estamos procurando forças, então começamos com diagrama de corpo livre.
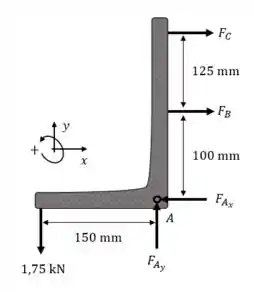
Vamos fazer equilíbrio dos momentos em , assim as reações e não contribuem e aí não precisamos nos importar com elas.
Duas incógnitas e uma equação. Vamos precisar de mais uma relação!
Passo 3
A barra vai girar ao redor do pino em . Como ela é rígida, ela não se deforma. Vejamos como os deslocamentos dos cabos se relacionam. A barra é a linha preta na figura.
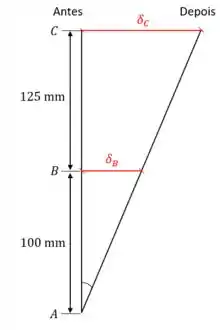
Temos dois triângulos com um ângulo em comum. Podemos formar uma equação com a tangente do ângulo:
Show! Com essa condição de compatibilidade podemos chegar em uma expressão que envolve as forças. Usando a relação carga-deslocamento
Passo 4
Substitua na condição de equilíbrio
Resposta
Força na corda em : .
Força na corda em : .