Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 214
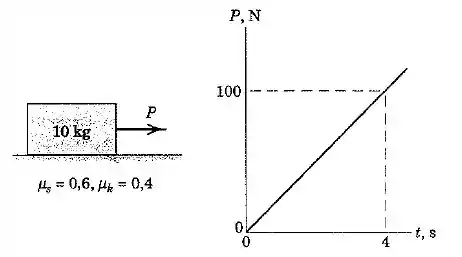
A força , que é aplicada ao bloco de inicialmente em repouso, varia linearmente com o tempo conforme indicado. Se os coeficientes de atrito estático e dinâmico entre o bloco e a superficie horizontal são e , respectivamente, determine a velocidade do bloco quando .
Passo 1
Vamos ver qual é a força mínima que deve ser exercida sobre o bloco para que ele começe seu movimento. Para isso, precisamos calcular a força de atrito máxima produzida pelo coeficiente de atrito estática:
Isso quer dizer que só veremos alguma aceleração () quando . Para descobrir em qual instante isso acontece, vamos encontrar a equação da reta:
E agora é só substituir para achar o valor de quando :
Passo 2
Ok, então quando teremos algum movimento, e devemos usar o coeficiente de atrito cinético. Nesse caso a força resultante será:
E então podemos usar o teorema do impulso para calcular a variação de velocidade:
E como o bloco parte do repouso:
Resposta
A velocidade do bloco em é