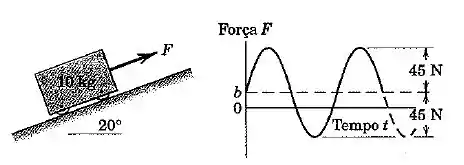
O carrinho de está parado no instante de tempo e posteriormente é submetido à força senoidal , onde e são expressos em newtons e o tempo é expresso em segundos. (a) Se , determine a velocidade do carrinho em . (b) Determine o valor de para o qual a velocidade do carrinho será zero após o primeiro ciclo completo de aplicação da força. Despreze o atrito.
Passo 1
Considerando que o carro parte do repouso, podemos usar o teorema do impulso para escrever a seguinte relação:
E as duas forças atuando sobre o bloco são:
Isso quer dizer que após um intervalo de tempo , a velocidade do carrinho será:
Passo 2
Primeiro precisamos entender o que é um ciclo completo dessa força. A função seno que aparece na fórmula da força é , isso quer dizer que o período da força é:
Esse é o tempo que um ciclo completo da força leva. Se queremos que a velocidade seja após esse intervalo, só precisamos retomar nossa equação de antes, mas com , e trocando os limites de integração.
Resposta
(a) .
(b) .