Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 3
6/3) A força é aplicada ao caixote de quando ele está em repouso . Determine o módulo e a direção da força de atrito exercida pela superfície sobre o caixote se (a) , (b) e (c) . (D) Que valor de é necessário para iniciar o movimento para cima no plano inclinado? Os coeficientes de atrito estático e dinâmico entre o caixote e o plano são e , respectivamente .
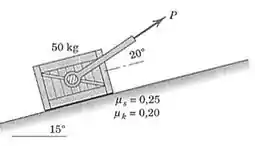
Passo 1
Então galera, como não ocorre movimento vertical , temos que :
Sendo assim , para :
Bom , agora assumindo equilíbrio , podemos aplicar o princípio do somatório das forças concorentes em relação ao eixo :
Logo ,
Para analisarmos se a hipótese de equilíbrio está certa , devemos calcular a força máxima de atrito pela relação :
Reparem que o valor de encontrado anteriormente é maior que o valor máximo da força de atrito estático , sendo assim o eu nós assumimos anteriormente está errado . Portanto ,
Passo 2
Utilizando raciocínio análogo ao do passo anterior , para , como não há movimento no eixo :
Sendo assim,
Assumindo equilíbrio , obtemos que :
A força máxima de atrito , por sua vez , é dada por :
Como , não há movimento e o que nós assumimos está certo .
Passo 3
Assim como nos passos anteriores , para , como não há movimento em :
Isolando , obtemos que :
Assumindo equilíbrio , achamos que :
A força máxima de atrito , por sua vez , é dada por :
Como , há movimento e que nós assumimos está errado . Portanto ,
Passo 4
Para iniciar o movimento , seja para baixo no plano inclinado , temos que :
Equilíbrio em relação ao eixo :
Equilíbrio em relação ao eixo :
Resposta
Respectivamente ,
Suave galera? Então bora próxima!!!