Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 118

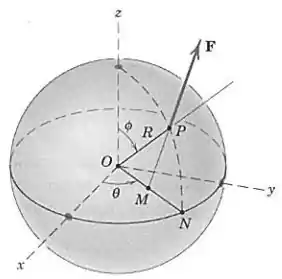
Uma força F é aplicada à superfície da esfera como mostrado. Os ângulos θ e ϕ localizam o ponto P e M é o ponto médio de O N . Expresse F em forma vetorial, usando as coordenadas x , y e z dadas.

Passo 1

Observe a figura a seguir:

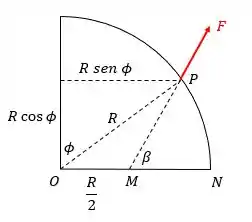
Note que podemos decompor a força desse modo:

F x = F x y cos ⁡ θ                   F y = F x y   s e n   θ                     F z = F   s e n   β

onde temos:

F x y = F cos ⁡ β

Logo, podemos expressar F vetorialmente assim:

F = F   [ cos ⁡ θ cos ⁡ β i + s e n   θ cos ⁡ β j + s e n   β   k ]

Passo 2

Assim, com base na figura, obtemos:

t g   β = R cos ⁡ ϕ R   s e n   ϕ - R 2 = 2 cos ⁡ ϕ 2   s e n   ϕ - 1

E portanto,

s e n   β = 2 cos ⁡ ϕ 2   s e n   ϕ - 1 2 + 2 cos ⁡ ϕ 2 = 2 cos ⁡ ϕ 5 - 4   s e n   ϕ

cos ⁡ β = 2   s e n   ϕ - 1 2   s e n   ϕ - 1 2 + 2 cos ⁡ ϕ 2 = 2   s e n   ϕ - 1 5 - 4   s e n   ϕ

Passo 3

Finalmente, podemos escrever:

F = F   [ cos ⁡ θ cos ⁡ β i + s e n   θ cos ⁡ β j + s e n   β   k ]

F = F   cos ⁡ θ 2   s e n   ϕ - 1 5 - 4   s e n   ϕ i + s e n   θ 2   s e n   ϕ - 1 5 - 4   s e n   ϕ j + 2 cos ⁡ ϕ 5 - 4   s e n   ϕ k

F = F 5 - 4   s e n   ϕ 2   s e n   ϕ - 1 cos ⁡ θ i + s e n   θ   j + 2 cos ⁡ ϕ k

Resposta

F = F 5 - 4   s e n   ϕ 2   s e n   ϕ - 1 cos ⁡ θ i + s e n   θ   j + 2 cos ⁡ ϕ k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cabo O A é usado para suportar a coluna O B . Determine o ângulo θ que ele forma com a viga O C .
Determine o ângulo θ entre os dois cabos presos ao poste.
O cabo O A é usado para suportar a coluna O B . Determine o ângulo ϕ que ele forma com a viga O D .
Determine as intensidades das componentes da força F = 400N que atuam na paralela e na perpendicular ao segmento B C do encanamento.
Cada cabo exerce uma força de 400N sobre o poste. Determine a intensidade da componente projetada de F 1 ao longo da linha de ação de F 2 .