Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 134
Determine o ângulo entre os dois cabos presos ao poste.
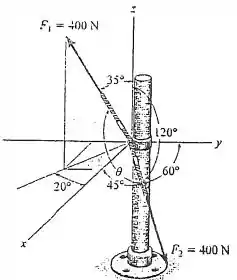
Passo 1
Para obter o ângulo desejado, é possível fazer a relação de produto escalar entre os vetores unitários de cada direção, ou seja, de e . Assim, o valor resultante será o cosseno do ângulo formado entre os dois segmentos e será determinado através função trigonométrica inversa.
Passo 2
Logo, os vetores unitários serão:
E:
Passo 3
Agora, fazendo o produto escalar entre os dois vetores unitários:
Passo 4
Logo, realizando a operação inversa do cosseno, tem-se que:
Resposta
Exercícios de Livros Relacionados
Encontre a intensidade da componente da força projetada ao longo do tubo.
Determine a intensidade, a direção e o sentido da força F → = 240N i → - 270N j → + ( 68 0N ) k → .
Uma barra de aço ABC é sustentada em parte pelo cabo DBE, que passa pelo anel B sem atrito. Sabendo que a tração no cabo é 1712 N, determine os componentes dessa força exercida pelo cabo no suporte em
Uma força atua na origem de um sistema de coordenadas na direção definida pelos ângulos θ y = 55 ° e θ z = 45 ° . Sabendo que a componente x da força é -2220N, determine, ( a ) o ângulo θ x , ( b ) os
Sabendo que a tração no cabo AC é 2130 N, determine a componente da força exercida na placa em C.