Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 123
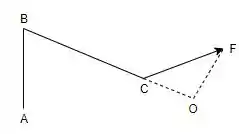
Determine as intensidades das componentes da força que atuam na paralela e na perpendicular ao segmento do encanamento.
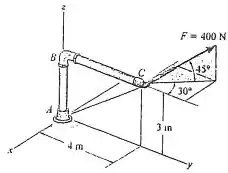
Passo 1
Para obter as componentes da força, o vetor força deve ser encontrado a fim de ela poder ser dividida pelas suas componentes.
Também, as relações de produto escalar devem ser relembradas.
Passo 2
Logo, a força será dada por:
E, portanto:
Passo 3
Para descobrir a intensidade da componente paralela ao segmento , pode ser realizado o produto escalar do vetor força com o vetor unitário que se encontra ao longo do segmento e é dado por . Com isso, tem-se que:
Passo 4
Agora, a intensidade da componente perpendicular ao segmento pode ser determinada através da relação do Teorema de Pitágoras, visto que a força e suas componentes formam um triângulo retângulo no qual e . Então:
