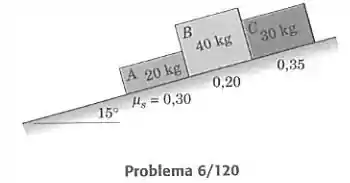
Três caixas em contato entre si são colocadas em um plano inclinado e são soltas a partir do repouso. Os coeficientes de atrito estático sob as caixas e valem 0,30, 0,20 e 0,35, respectivamente. Descreva o que ocorre.

Mas temos que descobrir o que acontece quando eles estão juntos. É claro que independente do que aconteça com os blocos e , vai ficar parado, pois ninguém empurra ele para baixo e ele satisfaz a condição de não deslizamento. Temos que analisar então a situação entre e . Vamos usar uma suposição, de que segura e então está na iminência de deslizar. Se obtivermos um coeficiente de atrito maior que 0,30 para , a suposição está errada e os dois blocos irão deslizar. Vamos separar e em diagramas de corpo livre. A força de atrito em será 0,20 vezes a normal pois o coeficiente de atrito é o estático, já que o bloco está na iminência de cair. No entanto, não sabemos ainda a relação entre a força de atrito e a normal em .

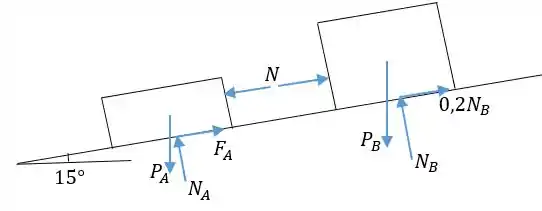
Primeiro vamos fazer as equações de equilíbrio para , para descobrir a força com a qual ele empurra o outro bloco. A direção é a direção paralela à rampa. Começamos fazendo na direção . A inclinação do peso em relação a essa direção é de 15°:

Agora fazemos na direção :

Agora vamos às equações para o corpo . Começamos novamente com a direção :

Agora na direção achamos o valor da força de atrito :

Agora que temos a força de atrito e normal em aplicadas pelo solo, vamos calcular o coeficiente de atrito:

Esse valor passa do coeficiente de atrito estático , portanto essa situação é impossível. Então tanto quanto irão deslizar.