Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 119
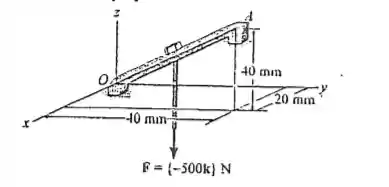
O grampo é usado em uma matriz. Se a força vertical que atua sobre o parafuso é , determine as intensidades de suas componentes que atuam ao longo do eixo e perpendicular a ele.
Passo 1
Desejamos encontrar as componentes da força orientada para o sentido negativo do eixo e perpendicular a ele. Sendo assim, vamos primeiramente encontrar o vetor unitário ao longo do eixo fazendo
Dessa forma, a projeção de ao longo do eixo será dada por
Já a componente perpendicular de será dada por
Resposta
Exercícios de Livros Relacionados
2.91 Encontre a intensidade, a direção e o sentido da resultante das duas forças mostradas, sabendo que P=300N e Q=400N.
2.97 A ponta de um cabo coaxial A E é fixada ao poste A B que é ancorado pelos fios A C e A D . Sabendo que a tensão do fio A C é 670N e a resultante das forças exercidas em A pelos fios A C e A D sev
No sentido de mover um caminhão acidentado, dois cabos foram fixados em A e puxados pelos guinchos B e C como mostrado na figura. Sabendo que a tração é 10 kN no cabo AB e 7,5 kN no cabo AC, determine
O comprimento do cabo AB é 20 m e a tensão neste cabo é 17350 N. Determine ( a ) as componentes x ,y e z da força exercida pelo cabo na âncora B, ( b ) os ângulos θ x ,θ y e θ z , definindo a direção
Dois cabos estão ligados juntos a C e carregados como mostra a figura. Determine a tensão ( a ) no cabo AC, ( b ) no cabo BC.