Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 52
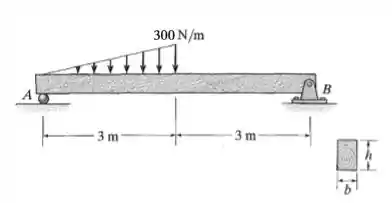
A viga simplesmente apoiada é feita de madeira com tensão de flexão admissível e tensão de cisalhamento admissível . Determine suas dimensões se ela tiver de ser retangular e a relação altura/largura tiver se ser .
Passo 1
Fala aí galera, vamos para mais uma resolução para você ficar craque nessa matéria. Este problema é simples e pequeno, só temos que ter atenção. Primeiramente, precisamos fazer o nosso querido DCL (Diagrama de corpo livre):
Passo 2
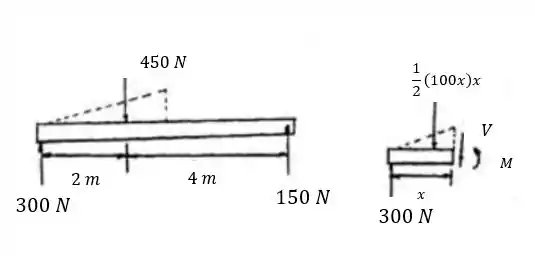
Com isso, vamos calcular as reações nos apoios:
Passo 3
O próximo passo é traçar os diagramas de força cortante e momento fletor:
E assim teremos o momento máximo dado por e a reação
Passo 4
Por fim, para encontrarmos as dimensões, vamos utilizar fornecido pelo enunciado, que é dado por:
Resposta
Exercícios de Livros Relacionados
Para a viga e o carregamento mostrado, determinar a maior tensão de cisalhamento na seção n-n.
A força cortante vertical é de 1200 lb em uma viga com a seção transversal mostrada na figura. Sabendo que d = 4 pol., Determine a tensão de cisalhamento no (a) ponto a, (b) ponto b..
Sabendo que uma dada força cortante vertical V causa uma tensão de cisaIhamento máxima de 50 MPa em um elemento de paredes finas com a seção transversal mostrada, determine a tensão de cisalhamento co
O cisalhamento vertical é de 1200 lb em uma viga com a seção transversal mostrando. Determine (a) a distância d para a qual a b, (b) o tensão de cisalhamento correspondente nos pontos a e b.
A viga de alumínio extrudada tem espessura de parede constante de in. Sabendo que a força cortante vertical na viga é de 2 kips, determine a tensão de cisalhamento correspondente em cada um dos cinco