Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 63
Uma força de compressão de 600 N deve ser aplicada às duas placas no punho da braçadeira C. O parafuso roscado tem um diâmetro médio de 10 mm e avança 2,5 mm por volta. O coeficiente de atrito estático é de 0,20. Determine a força F que deve ser aplicada normal à alça em C, a fim de (a) apertar e
(b) afrouxe a braçadeira. Despreze o atrito no ponto A
Passo 1
(a) A equação do momento de equilíbrio é
(1)
Em que W é a força compressiva axial
R é o raio
α é o ângulo que a rosca faz com o eixo y, uma vez que a rosca se move 2,5 mm por revolução, e a circunferência de um círculo é 2rπ, podemos determinar α
Podemos determinar o ângulo uma vez que conhecemos o coeficiente de fricção
Passo 2
Finalmente, colocando todos os valores conhecidos na equação (1), vamos determinar M
Uma vez que o comprimento do braço BC é 100 mm, a força aplicada a ele deve ser
Passo 3
(b) Observe que ao tentar afrouxar o dispositivo, a força de atrito terá direção oposta, portanto o ângulo que R resultante faz com o eixo x é (ϕ-α), portanto a equação de equilíbrio de momento é
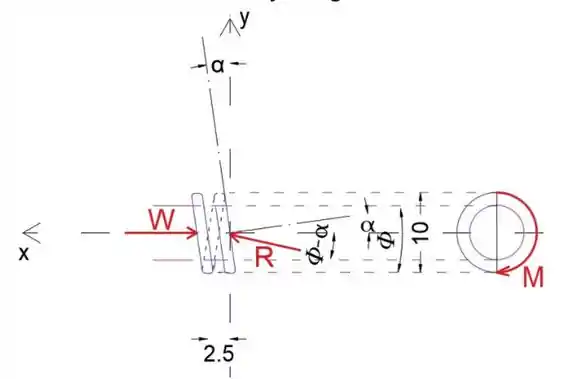
Como os parâmetros W, r, ϕ e α são os mesmos da parte a) do problema, colocando todos os valores conhecidos na equação (1), determinaremos M
Uma vez que o comprimento do braço BC é 100 mm, a força aplicada a ele deve ser
Resposta
a) b)