Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 33
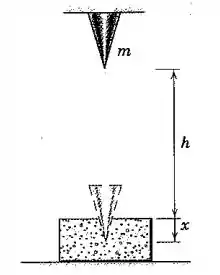
Em um teste para determinar as características de esmagamento de embalagens de poliestireno, um cone de aço de massa é largado de modo que caia uma distância e então penetre no material. A resistência do poliestireno à penetração depende da área da seção transversal do objeto penetrante e, portanto, é proporcional ao quadrado da distância de penetração de cone, ou . Se o cone atinge o repouso em uma distância , determine a constante em termos das condições do ensaio e dos resultados.
Passo 1
Pessoal, ao cair uma distância , o cone adquire uma velocidade que chamaremos de , calculada assim:
A partir daí, além do peso, passa a atuar a força de resistência , em sentido contrário. Aplicando a Segunda Lei de Newton:
Passo 2
Como temos a aceleração em função de , podemos utilizar a seguinte equação diferencial:
Integrando cada lado:
Passo 3
Para calcular o valor da constante , substituímos , como já calculamos, e também para , pois o cone atinge o repouso aí: