Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 11

Que força de módulo deve a pessoa aplicar no cabo, para fazer com que a leitura na balança seja de ? Os pesos das polias e cabos são desprezíveis. Descreva qualquer hipótese feita.

Passo 1

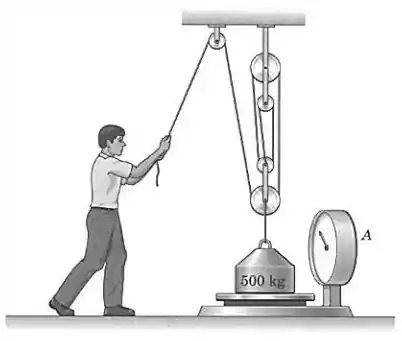
Vamos lembrar que a força de módulo está sendo transmitida para todo o cabo, e esse cabo passa por todas as polias. Ou seja, no final das contas, a massa de está sendo puxada para cima por uma força equivalente a proveniente do cabo, pois são partes do cabo puxando o sistema, olha só:

Nesse caso, estamos assumindo a hipótese de que cada parte do cabo fica totalmente vertical, caso contrário haveria componentes das forças na horizontal, e então a força para cima seria menor do que .

Passo 2

Além disso, a massa ainda sofre a ação do seu próprio peso (para baixo) e da reação normal (para cima) de , que é a leitura da balança. Escrevemos então a equação de equilíbrio de forças na vertical:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para testar a deflexão da viga uniforme de 100k g , o garoto de 50k g dá um puxão de 150N na corda, como mostrado. Calcule a força suportada pelo pino na dobradiça O .

Determine as reações externas em A e F para a treliça de um telhado carregada como mostrado. As cargas verticais representam o efeito de sustentação dos materiais do telhado, enquanto a força de 400N

O carro completo, com seu motorista, tem massa de 815k g e, sem os dois aerofólios, tem uma distribuição de peso igual ( 50 % - 50 % ) entre a dianteira e a traseira em uma dada velocidade na qual o c

O elemento O B C e a roldana em C , juntos, têm uma massa de 500k g , com um centro de massa combinado em G . Calcule o módulo da força suportada pela conexão de pino em O quando a carga de 3k N é apl

A porta de carga de um avião com fuselagem circular consiste de um segmento uniforme A B de um quarto de círculo e massa m . Uma trava na dobradiça em A mantém a porta aberta na posição mostrada. Dete