Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 52
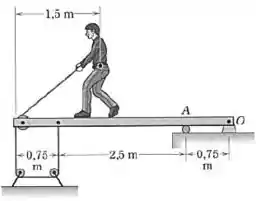
Para testar a deflexão da viga uniforme de , o garoto de dá um puxão de na corda, como mostrado. Calcule a força suportada pelo pino na dobradiça .
Passo 1
Vamos começar escrevendo as seguintes equações de equilíbrio:
Temos 6 forças atuando na viga: duas tensões de ( a localizada no final da viga apontando para baixo (repara que tem uma roldana, então a força que ele faz é igual à tração do outro lado, que é pra baixo) e a outra para baixo) , o peso do garoto e o peso da viga (ambas apontando para baixo) e as forças de reação nos suportes A e O. Vamos escrever uma expressão para os momentos dessas quatro forças.
Vamos usar a primeira equação de equiíbrio, o momento nulo em O:
Passo 2
Usando a outra equação de equilíbrio:
Resposta
A força no pino deve ser .
Exercícios de Livros Relacionados
Um homem com peso de 875 N( ≈ 87,5 k g ) tenta se suspender usando um dos dois métodos mostrados. Determine a força total que ele precisa exercer na barra A B em cada caso e a reação normal que ele ex
Um homem com peso de 875 N( ≈ 87,5 k g ) tenta se suspender usando um dos dois métodos mostrados. Determine a força total que ele precisa exercer na barra A B em cada caso e a reação normal que ele ex
O guincho é usado para suspender o motor de 200k g . Determine a força que atua no cilindro hidráulico A B , as componentes horiozntal e vertical da força no pino C e as reações no apoio fixo D .
Dois cabos estão ligados em C e são carregados como mostra a figura. Determine a tração (a) no cabo A C e (b) no cabo B C .
Dois cabos estão ligados em C e são carregados como mostra a figura. Determine a tração ( a ) no cabo AC e ( b ) no cabo BC.