Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 58
A porta de carga de um avião com fuselagem circular consiste de um segmento uniforme de um quarto de círculo e massa . Uma trava na dobradiça em mantém a porta aberta na posição mostrada. Determine o momento exercido pela dobradiça sobre a porta.
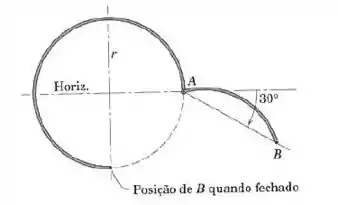
Passo 1
A principal força agindo aqui é o peso do arco (quarto de círculo) . Podemos olhar a tabela no final do livro para encontrar o centro de massa de um arco como esse, e então vamos saber onde a força atual.
A fórmula mais geral para o centro de massa de um arco é:
Como estamos lidando com um quarto de círculo, temos . ( é a metade do ângulo do arco).
Passo 2
Agora que sabemos o ponto onde a força atua podemos calcular o momento gerado por ela. Para que a situação da figura esteja em equilíbrio, o momento gerado pela dobradiça deve ser igual ao dessa força.
O grande desafio de calcular o momento gerado pelo peso é encontrar uma expressão para a distância perpendicular entre e o ponto de aplicação dessa força. No desenho, vamos representar isso pela linha vermelha:
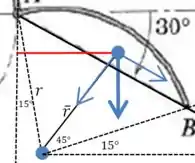
Podemos escrever o comprimento da linha vermelha da seguinte forma:
Agora podemos exigir aquela igualdade para os momentos (o da força e o da dobradiça):
Resposta
O momento exercido pela dobradiça é .