Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 25
A barra AB é fixada ao bloco A que desliza sem atrito na fenda vertical como mostrada na figura. Desprezando o efeito do atrito e o peso das barras, determine o valor de correspondente ao equilíbrio.
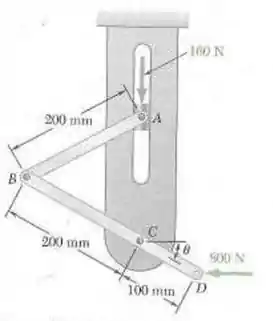
Passo 1
Essa questão é bem simples galera! Primeiro, temos que:
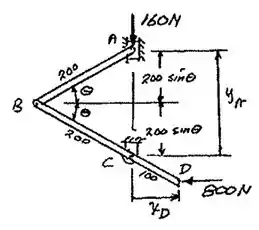
Passo 2
Aplicando o trabalho virtual:
Resposta
Exercícios de Livros Relacionados
Uma barra delgada de comprimento l e peso W é pivotada em uma extremidade como mostra a figura. Ela é liberada do repouso na posição horizontal e oscila livremente. (a) Determine a velocidade angular
A elevação da plataforma de massa m suportada pelos quatro elos idênticos é controlada pelos cilindros hidráulicos AB e AC que são articulados no ponto A. Determine a compressão P em cada um dos cilin
A aceleração de uma partícula é diretamente proporcional ao tempo t . Quando t = 0 , a velocidade da partícula é v = 16 m / s . Sabendo que v = 15 m / sex = 20 m quando t = 1 s , determine a velocidad
Determine o valor de equilíbrio de x para a barra sustentada por molas. A mola tem uma rigidez ke não é esticada quando x = 0. A força F atua na direção da barra, e a massa da barra é desprezível.
Para o mecanismo mostrado, a mola é descomprimida quando θ = 0. Determine o ângulo θ para a posição de equilíbrio e especifique a rigidez mínima da mola k que limitará θ a 〖30〗 ^ ∘. A haste DE passa l