Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 18

Se a força P=4kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

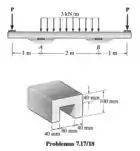
Passo 1

Vamos começar calculando as reações de apoio.

∑ M B = 0 ⇒ 3 ⋅ P - R A ⋅ 2 + 3 ⋅ 2 ⋅ 1 - 1 ⋅ P = 0

2 ⋅ 4 - 2 R A + 6 = 0

R A = 7

∑ F y = 0 ⇒ - P + R A - 3 ⋅ 2 + R B - P = 0

R B = 7

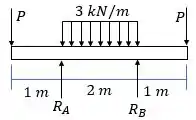
Passo 2

Agora utilizamos o método gráfico para gerar o diagrama de momento fletor:

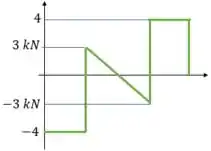
Perceba que a maior força de cisalhamento na viga é V = 4

Passo 3

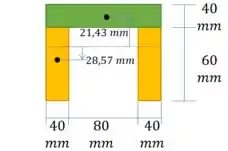
Vamos olhar agora pra seção. Primeiro vamos definir o centroide:

y C = A v e r d e y v e r d e + 2 A a m a r e l a y a m a r e l a A v e r d e + 2 A a m a r e l a

y C = 40 ⋅ 160 ⋅ 80 + 2 ⋅ 60 ⋅ 40 ⋅ 30 40 ⋅ 160 + 2 ⋅ 60 ⋅ 40

y C = 58,57   m m

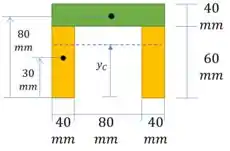
Passo 4

E agora podemos calcular o momento de inércia:

I = I v e r d e + 2 ⋅ I a m a r e l o

I = 160 ⋅ 40 3 12 + 40 ⋅ 160 ⋅ 21,43 2 + 2 ⋅ 40 ⋅ 60 3 12 + 60 ⋅ 40 ⋅ 28,57 2

I = 9,15 ⋅ 10 6   m m 4

Passo 5

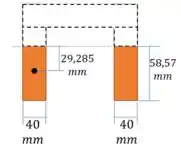
Agora vamos calcular o momento estático máximo. Para esse caso é mais simples calcular a área abaixo do centroide.

Q = 58,57 ⋅ 2 ⋅ 40 ⋅ 29,285

Q = 137217,796   m m 3

Passo 6

E finalizamos a questão aplicando a Equação 7.3

τ = V Q I t

Vamos substituir os valores. Mas tenha atenção, pois o nosso momento estático é composto por duas “perninhas” da viga, cada uma com espessura. Isso quer dizer que: t = 2 ⋅ 40

τ = 4   k N ⋅ 137217,796   m m 3 9,15 ⋅ 10 6   m m 4 ⋅ 2 ⋅ 40   m m

Isolando o P :

τ = 0,75   M P a

Resposta

τ = 0,75   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cisalhamento vertical é de 1200 lb em uma viga com a seção transversal mostrando. Determine (a) a distância d para a qual a  b, (b) o tensão de cisalhamento correspondente nos pontos a e b.
A viga de alumínio extrudada tem espessura de parede constante de in. Sabendo que a força cortante vertical na viga é de 2 kips, determine a tensão de cisalhamento correspondente em cada um dos cinco
Quatro cantoneiras de aço 1,202 x 102 x 9,5 e uma placa de 12 x 400 mm são parafusadas de modo a formar a viga de seção transversal mostrada. Os parafusos tem diâmetro de 22mm e são espaçados longitud
Saber que um determinado cisalhamento vertical V causa uma tensão de cisalhamento máxima de 75 MPa em uma viga extrudada tendo a seção transversal mostrada, determine o tensão de cisalhamento nos três
Uma coluna é fabricada conectando-se os perfis de aço laminado mostrados na figura por parafusos de 19,05 mm de diâmetro espaçados longitudinalmente a cada 190,5 mm. Determine a tensão de cisalhamento