Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 4

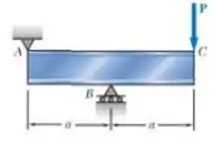
Uma viga biapoiada com um balanço de aço laminado com um balanço de aço laminado W 920   ×   449 suporta uma carga P conforme mostra a figura. Sabendo que P = 850   k N , a = 2,0   m   e   e   σ a d m = 100   M P a , determine (a) o valor máximo da tensão normal σ m na viga (b) o valor máximo da tensão principal σ m á x na junção da mesa com a alma e (c) se o perfil especificado é aceitável no que se refere a essas duas tensões.

Passo 1

E ai gurizada tudo bem, o enunciado pede que a gente determine o valor máximo da tensão normal σ m na viga, o valor máximo da tensão principal σ m á x na junção da mesa com a alma e se o perfil especificado é aceitável, vamos aos dados do enunciado :D

V m á x = 850   k N   =   850   ×   10 3   N

M m á x = ( 850   ×   10 3 ) ( 2,0 ) = 1,70   ×   10 6   N ⋅ m

Para   W 920 × 449 seção de aço laminado,

d = 947   m m b f = 424   m m t f = 42,7   m m

t w = 24,0   m m , I X = 8780   ×   10 6   m m 4 , S X = 18,500 × 10 3   m m 3

c = 1 2   d = 473,5   m m y b = c   - t f = 430,8   m m

Passo 2

Agora sim gurizadaa vamos encontrar o valor máximo da tensão normal σ m na viga, vem comigo :D

(a) σ m = M m a x S X = 1,75   ×   10 6 18,500 × 10 - 6 = 94,595   M P a σ m = 94,6   M P a

σ b = y b C   σ m = 430 473,5 ( 91,892 ) = 83,605   M P a

A área da seção é determinada por:

A f = b f   t f = 18,1048   ×   10 3   m m 2

y _ f = 1 2 ( c +   y b ) = 452,15   m m

Q b = A f   y _ f = 8186,1   ×   10 3   m m 3 = 8186,1   ×   10 - 6   m 3

Agora temos que determinar a tensão de cisalhamento, mas é tranquilinho é apenas aplicando na equação a seguir :D

τ x y = V m a x Q b I x t w = (   850 ×   10 6 ) ( 8186,1   ×   10 - 6 ) ( 8780   ×   10 - 6 ) ( 24,0   ×   10 - 3 ) = 33,021   M P a

R = σ b 2 2   +   t x y 2 = 83,605 2 2   + 33,021 2 = 53,271   M P a

Passo 3

Agora vamos encontrar valor máximo da tensão principal σ m á x na junção da mesa com a alma, então temos que utilizar σ b calculada por nós no passo 1 :D

(b) σ m a x = σ b 2 + R = 83,605 2 + 53,271 = 95,1   M P a

σ m a x = 95,1   M P a

Passo 4

Por último e não menos importante precisamos determinar se o perfil especificado é aceitável

(c) Desde a 95,1   M P a   < σ a l l ( = 100   M P a ) ,

W 920   ×   449     é   a c e i t á v e l

Resposta

  1. 83,605   M P a
  2. 95,1   M P a
  3. é   a c e i t á v e l
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que σ a d m = 160M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar carga mostrada. (b) Determine os valores a serem esperados pa
Sabendo que σ a d m = 160M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar o carregamento mostrado. () Determine os valores a serem espe
Os problemas a seguir, se referem a um perfil de aço laminado selecionado em um problema do capítulo 5, para suportar determinado carregamento a um custo mínimo e ao mesmo tempo satisfazendo a condiçã
Os problemas a seguir, se referem a um perfil de aço laminado selecionado em um problema do capítulo 5, para suportar determinado carregamento a um custo mínimo e ao mesmo tempo satisfazendo a condiçã
Os problemas a seguir, se referem a um perfil de aço laminado selecionado em um problema do capítulo 5, para suportar determinado carregamento a um custo mínimo e ao mesmo tempo satisfazendo a condiçã