Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 2

Uma viga de aço laminado W 250   ×   58 suporta uma carga P conforme mostra a figura. Sabendo que P =   100   k N , a = 508   m m   e   σ a d m = 124,1   M P a determine (a) o valor máximo da tensão normal σ m na viga,(b) o valor máximo da tensão principal σ m á x na junção da mesa com alma e (c) se o perfil especificado é aceitável no que se refere a essas duas tensões.

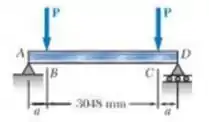
Passo 1

Então gurizada, tudo bem com vocês? O enunciado pede que a gente determine o valor máximo da tensão normal σ m na viga, o valor máximo da tensão principal σ m á x na junção da mesa com alma e se o perfil especificado é aceitável no que se refere a essas duas tensões vamos fazer. Então bora lá!

Vamos a algumas conversões para facilitar, ok!?

P = 200   k N = 45   k i p s a = 254   m m = 10   i n

σ A D M = 124,1   M P a = 1 = 8   k s i

Abaixo temos um esboço do diagrama de corpo livre para facilitar o entendimento dos cálculos :D

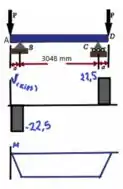
Agora, vamos aos cálculos:

V t o t a l = 22,5   k i p s M t o t a l = ( 22,5 ) ( 20 ) = 450   k i p s ⋅ i n

Para seção w 250 × 58 de aço laminado:

d = 9,92   i n b f = 7,99   i n t f = 0,530   i n t w = 0,325   i n

I x = 209   i n 4 S x = 42,1   i n 3 c = 1 2 d = 4,96   i n y b = c - t f = 4,43   i n

Passo 2

Agora simm podemos determinar o valor máximo da tensão normal σ m na viga, então basta aplicar na equação abaixo para começarmos :D

σ m = M t o t a l S x = 450 42,1

σ m = 10,69   k s i = 73,7   M P a

σ b = y b c σ m = 4,43 4,96 ( 10,69 ) = 9,55   k s i

Temos então que determinar a área ....

A f = b f t f = 4,2347   i n 2

y _ f = 1 2 c + y b = 4,695   i n Q b = A f y _ f = 19,8819   i n 3

A tensão de cisalhamento é dada por:

τ x y = V t o t a l Q b I x t w = ( 22,5 ) ( 19,8819 ) ( 209 ) ( 0,315 ) = 6,7949   k s i

R = ( σ b 2 ) 2 + τ x y 2 = 8,3049   k s i

Passo 3

Então agora temos que encontrar o valor máximo da tensão principal σ m á x na junção da mesa com alma

σ t o t a l = σ b 2 + R = 9,55 2 + 8,3049 = 13,08   k s i

σ t o t a l = 13,08   k s i =   90,2   M P a

Passo 4

Agora podemos ver se o perfil especificado é aceitável no que se refere a essas duas tensões

Desde que:

σ t o t a l > σ t u d o ( = 18   k s i )

w 250 × 58 é aceitável

Resposta

(a) σ m = 10,69   k s i = 73,7   M P a

(b) σ t o t a l = 13,08   k s i =   90,2   M P a

(c) é aceitável.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Assumindo que as intensidades das forças aplicadas aos discos A e C do Prob. 8.19 são ,respectivo, P 1 = 1080l b e P 2 = 810l b ,e utilizando a expressão dada no Prob. 8.21, determine os valores de τ
Os eixos de seção transversal cheia ABC e DEF e as engrenagens mostradas são utilizados para transmitir 20h p do motor M para uma máquina-ferramenta conectada ao eixo DEF. Sabendo que o motor gira a 2
Considerando que eixo ABC do Problema 8.27 é vazado e tem um diâmetro externo de 50m m ,determine o maior diâmetro inteiro admissível para o eixo
O eixo de seção cheia AB rotaciona a 600r p m e transmite 80k W a partir do motor M para a máquina-ferramentas conectadas à engrenagem F.Sabendo que τ a d m= 60M P a ,determine o menor diâmetro permit
O eixo de seção cheia ABC e as engrenagens mostradas na figura transmitem 10k W do motor M para uma máquina-ferramenta conectada à engrenages D . Sabendo que o motor gira 240r p m e que τ a d m = 60M