Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 16

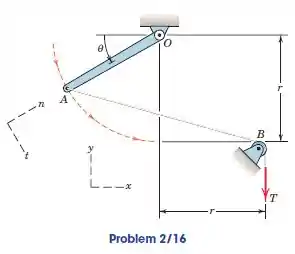
Determine as componentes x e y da força trativa T que é aplicada no ponto A da barra O A . Despreze os efeitos da pequena polia em B . Assuma que r e θ são conhecidos.

Passo 1

Olá, tudo joinha?

Neste problema, precisamos encontrar as componentes x e y da força trativa T que é aplicada no ponto A . Observe a figura:

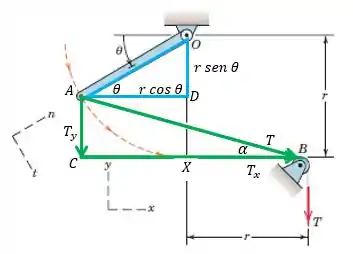
Vamos lá!

De início, já vemos que:

T x = T cos ⁡ α

T y = - T   s e n   α

Fizemos ali dois triângulos retângulos, vamos falar de cada um deles. Primeiro o triângulo azul:

Veja que a barra O A - tem comprimento igual ao do raio, r ,

O A - = r

Então,

O D - = r   s e n   θ

A D - = r cos ⁡ θ

Passo 2

Agora, analisando o triângulo verde.

A C - = D X -

Então,

A C - = O X - - O D -

A C - = O X - - r   s e n   θ

Veja que,

O X - = r

Portanto,

A C - = r - r   s e n   θ

A C - = r   ( 1 - s e n   θ )

Olhando para o segmento B C - :

B C - = A D - + r

Como A D - = r cos ⁡ θ :

B C - = r cos ⁡ θ + r

B C - = r   ( 1 + cos ⁡ θ )

Passo 3

Para encontrar o segmento A B - vamos aplicar o Teorema de Pitágoras:

A B - 2 = A C - 2 + B C - 2

A B - = r   ( 1 - s e n   θ 2 + r   ( 1 + cos ⁡ θ ) 2

A B - = r 2 1 - s e n   θ 2 + r 2 ( 1 + cos ⁡ θ ) 2

A B - = r 2 [ 1 - s e n   θ 2 + 1 + cos ⁡ θ 2 ]

A B - = r 1 - s e n   θ 2 1 + cos ⁡ θ 2

A B - = r   1 + s e n 2   θ - 2   s e n   θ + 1 + cos 2 ⁡ θ + 2 cos ⁡ θ

Sabemos que,

s e n 2 θ + cos 2 ⁡ θ = 1

Então,

A B - = r   1 + 1 + 1 - 2   s e n   θ + 2 cos ⁡ θ

A B - = r   3 - 2   s e n   θ + 2 cos ⁡ θ

Passo 4

Calma que está quase acabando! Haha! Já podemos encontrar as componentes T x e T y . Veja que,

cos ⁡ α = B C - A B -

s e n   α = A C - A B -

Fazendo a substituição,

T x = T cos ⁡ α

T x = T B C - A B -

T x = T r   ( 1 + cos ⁡ θ ) r   3 - 2   s e n   θ + 2 cos ⁡ θ

T x = T   ( 1 + cos ⁡ θ ) 3 - 2   s e n   θ + 2 cos ⁡ θ

Encontramos T x , só falta T y :

T y = - T   s e n   α

T y = - T   A C - A B -

T y = - T r   ( 1 - s e n   θ ) r   3 - 2   s e n   θ + 2 cos ⁡ θ

T y = T   ( s e n   θ - 1 ) 3 - 2   s e n   θ + 2 cos ⁡ θ

Resposta

T x = T   ( 1 + cos ⁡ θ ) 3 - 2   s e n   θ + 2 cos ⁡ θ

T y = T   ( s e n   θ - 1 ) 3 - 2   s e n   θ + 2 cos ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

185- Uma bóia de marcação consistindo de um cilindro e um cone tem as dimensões mostradas e tem uma massa de 285k g . Determine a altura h quando a bóia está flutuando em água salgada. A bóia é constr
186- Um canal de água doce com 3m de largura (normal ao plano do papel) está bloqueado na sua extremidade por uma barreira retangular, A B D , mostrada em seção. Escoras B C estão espaçadas a cada 0.6
188- Uma esfera sólida e homogênea de raio r está apoiada sobre o fundo de um tanque que contém um líquido de massa específica ρ l , que é maior do que a massa específica ρ s da esfera. A medida que o
187- Uma seção vertical de um tanque para drenagem do óleo está mostrada. A placa de acesso cobre uma abertura retangular, que tem uma dimensão de 400m m normal ao plano do papel. Calcule a força tota
192- Determine a força total R exercida sobre a janela triangular pela água doce no tanque. O nível da água coincide com o topo da janela. Determine, também, a distância H , desde R até o nível da águ