Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 13
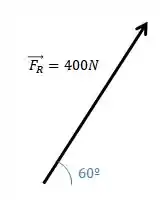
Se a tração no cabo é , determine a intensidade e a direção da força resultante que atua sobre a polia. Esse ângulo é o mesmo ângulo θ da linha AB no bloco do carretel.
Passo 1
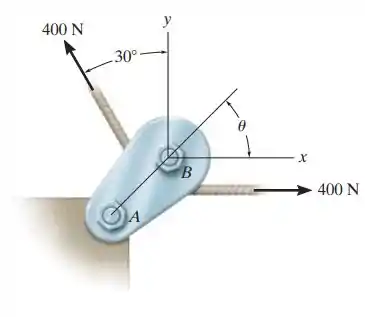
Fala ai galerinha bonita, xuxu beleza? Nesse exercício o enunciado nos diz que temos duas forças atuando sobre uma polia através de um cabo com intensidade de de acordo com a figura abaixo:
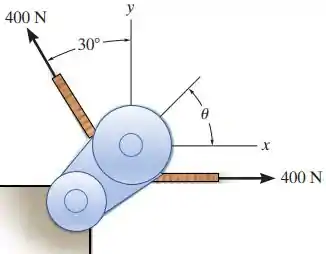
Para este problema vamos resolver utilizando a regra do paralelogramo, olha. Vamos analisar os vetores, estendendo-os para formar um paralelogramo.
Passo 2
Daqui podemos extrair o seguinte triângulo
Repara que, por ser um paralelogramo, os lados paralelos são iguais. Por isso o lado da direita também vale , de acordo com a primeira figura e faz um ângulo de .
Vamos começar calculando a magnitude da força, para isso vamos usar a soma vetorial dos vetores, dada através da lei dos cossenos, saca só:
Se liga, que esse é o ângulo entre as forças e , olhando para o desenho da questão, podemos ver que ele vale:
Substituindo vamos ter:
Opa, portanto, temos um triângulo com todos os lados iguais.
E no triângulo equilátero, todos os ângulos valem . Sendo assim, encontramos o ângulo da nossa força resultante.
