Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 138
Uma força de é aplicada à extremidade da chave, quando a polia dentada é presa a biela de um motor. A força é perpendicular ao plano contendo os pontos , e . Determine o momento dessa força em relação ao ponto .
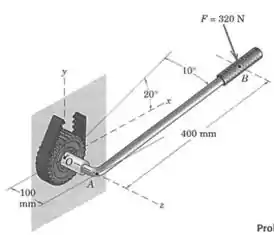
Passo 1
Vamos começar escrevendo a força em forma vetorial:
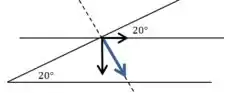
Passo 2
Agora vamos escrever o vetor posição que liga os pontos e :
Passo 3
E agora podemos calcular o momento da força fazendo o produto vetorial:
Resposta
O momento total em relação a é .
Exercícios de Livros Relacionados
O caminhão mostrado é usado para entregar refeições para aviões. A unidade elevada tem uma massa de 1000 kg, com centro de massa em G . Determine a força necessária no cilindro hidráulico A B .
Determine a força de compressão C exercida sobre a lata para uma força aplicada P = 50N quando o esmagador de latas está na posição mostrada. O ponto B está centrado no fundo da lata.
Uma ponte rolante para transportar tambores de aço de 135 kg é mostrada. Calcule o módulo da força exercida no tambor em E e F .
Detalhes adicionais da caçamba do guindaste do Prob. 4/111 estão dados na figura. Determine a força do cilindro H J devido aos efeitos da massa combinada de 180 kg da caçamba e do operador, com centro
Determine a força no cilindro A B devida ao peso combinado da caçamba e do operador. A massa combinada é de 180 kg, com centro de massa em G .