Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 26
A forma original da peça de borracha é retangular e ela é submetida à deformação mostrada pelas linhas tracejadas. Determine a deformação normal média ao longo da diagonal DB e do lado AD.
Passo 1
Podemos então calcular algumas distâncias e os ângulos de deformação:
Representando os dados calculados:
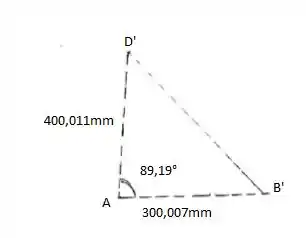
Passo 2
Podemos calcular, por lei dos cossenos, B’D’:
Passo 3
E agora é só calcularmos as doformações:
-3
Resposta
-3
Exercícios de Livros Relacionados
6.128 e 6.129 Em um ponto da superfície de uma placa fina foi determinado o estado de deformações. Sabendose que a superfície da placa está isenta de tensões e o coeficiente de Poisson é 0,30, determi
6.128 e 6.129 Em um ponto da superfície de uma placa fina foi determinado o estado de deformações. Sabendose que a superfície da placa está isenta de tensões e o coeficiente de Poisson é 0,30, determi
Um quadrado ABCD de 50mm de lado é riscado sobre a superfície de uma placa fina, quando a placa está sem carga. Depois da placa ser carregada, observou=se que os comprimentos dos lados AB e AD foram a
No P r o b . 6.100 , determinar o máximo valor admissível para h , sabendo-se que a tubulação é feita de um aço com uma tensão ultima a tração de 450M p a e que um coeficiente de segurança de 4,50 é d
Para o reservatório de ar comprimido do P r o b . 6.104 , determinar a maior pressão admissível, sabendo-se que a tensão normal admissível perpendicular a solda é de 165M p a e a tensão admissível de